
,
Замечания к публикации
Книга Дж. Норвуда была выложена на сайте в 2006 г. в виде отсканированных страниц, ради экономии места сильно сжатых и поэтому трудно читающихся. Отмечу, что лет через 10 на сайте seatracker появилась раздача с более высоким разрешением.
Cильная сторона книги — аналитический подход, но множество выкладок, хотя и не выходящих за рамки школьной алгебры и тригонометрии, делают книгу трудным чтением и подталкивают нетерпеливого читателя сразу перейти к выводам. Можно поступать и так, а дотошный конструктор или разработчик парусных симуляторов разберутся повнимательнее. В качестве дополнения к работе Норвуда порекомендую книгу Дж. Летчера "Самостоятельное подруливание парусного судна", в которой детально рассмотрены действующие на яхту силы и курсовая устойчивость, причем почти без математики, с упором на наглядную физическую картину.
Написанная в 1979 г. книга Норвуда заслуживает того, чтобы быть доступной для конструкторов-самодельщиков и сейчас. Спустя 18 лет публикацию решено было улучшить и сделать доступным ее содержание для поисковых систем, распознав текст и сделав html-вариант.
В данной публикации британские единицы заменены на метрические, кроме скорости в узлах и длины лодок в футах там, где речь идет о "футовых" классах, а также в британских критериях DLR и SLR. Простые формулы переведены в символьную запись, более громоздкие оставлены в виде картинок, увы, как они и были — низкого качества. AS IS. Если найдется читатель, который окажется не в силах разобраться с важными для себя "крякозябрами" — ему придется самому поработать с более качественными сканами... или оплатить работу по корректировке.
ГШ, 2024 г.

,
ББК 39.427
Н82
УДК 629.125.12
Рецензент докт. техн. наук Ю.С. Крючков
Научный редактор канд. техн. наук К.В. Рождественский
© 1979, Granada Publishing
© Перевод на русский язык, издательство "Судостроение", 1983 г.
1. Физические основы достижения высоких скоростей под парусами
2. Корпуса и аутригеры
3. Конструкция корпуса
4. Паруса и поперечная остойчивость
5. Сопротивление дрейфу и управляемость
6. Подводные крылья
7. Мореходность и безопасность плавания
8. Ходовые качества
9. Катамараны
10. Тримараны
11. Проа
Заключение
Приложения
Определение параметров хода яхты при постоянном β
Принятые обозначения
Использование силы ветра для движения судов восходит к античным временам. С началом технической революции и применения дешевого топлива паруса ушли с коммерческих океанских линий, наряду с этим иссяк источник правительственных субсидий на исследования в области парусного судостроения. Единственным исключением были спортивные суда, конструкции которых продолжали создавать и совершенствовать.
Период от заката больших парусников до наших дней отмечен достижениями во всех сферах науки и техники. Авиация прошла путь от первых хрупких сооружений до сверхзвуковых самолетов; одновременно в результате широко проводимых исследований обогатились наши знания в области аэродинамики. Появились новые материалы, по своим качествам превосходящие сталь и другие традиционные судостроительные материалы. В результате использования научно-технических достижений были созданы парусники, превзошедшие все, что было известно о этой области до сих пор.
Вместе с тем в настоящее время научно обосновано и практически осуществлено возрождение торговых парусных судов, эксплуатация которых рентабельна и перспективна в условиях исчерпания мировых запасов нефти. Однако не будем останавливать внимание на судах подобного типа, а ограничимся рассмотрением парусных яхт, длина которых нс больше 30 м. Речь пойдет о многокорпусных парусных судах, превосходящих по скорости хода обычные яхты.
О парусных яхтах написано достаточно работ, содержащих качественные или эмпирические данные, и совсем мало работ, в которых можно было бы найти аналитические данные. Накоплен большой опыт по яхтам классической конструкции, но совсем нелегко получить даже основные сведения о многокорпусных парусниках. Причина заключается в том, что проблему работы паруса и общем виде до сих пор нельзя считать решенной, во-первых. потому что ей трудно найти исчерпывающее определение, во-вторых, даже при наличии адекватного определения не представляется возможным получить аналитическое решение в связи с нелинейностью задачи. При своей способности ходить без крена многокорпусные суда представляют собой более подходящий объект для анализа, чем обычные яхты.
В книге использован определенный математический аппарат, который за небольшим исключением не выходит за рамки элементарной алгебры и тригонометрии. Математика дана для полноты и достоверности изложения. Выводы, сделанные с ее помощыо, проанализированы и представлены в табличной форме, в виде графиков и диаграмм. Книга требует серьезного внимания, однако наличие математических зависимостей не должно препятствовать пониманию физической картины явлений.
Именно с рассмотрения физических основ движения парусного судна и начинается книга. В дальнейшем исследуется влияние конструктивных особенностей судна на его ходовые качества, приводятся количественные зависимости скорости судна от его основных характеристик, силы и направления ветра и, в заключение, описаны типы многокорпусных парусных судов, даны перспективы их развития. Обозначения, использованные в формулах, объясняются в приложении.
Joseph Norwood, Jr.
Oriental, N. С.
Парусные суда используют для своего движения разницу в скорости перемещения потоков воды и воздуха, существующую на границе их раздела. Скорость ветра представим вектором VТ (истинный ветер), величина которого равна скорости воздушного потока относительно воды. Под действием силы ветра судно движется со скоростью VВ в направлении, заданном вектором VВ Движение объекта со скоростью VВ индуцирует встречный ветер с такой же скоростью. Скорость воздушного потока, действующего на судно (вымпельный ветер), выразится суммой векторов скоростей истинного и индуцированного ветра.
VA = VT + VВ
| (1.1) |
Это векторное уравнение может быть представлено геометрически (рис. 1.1).
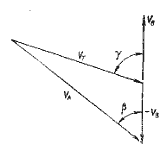
Рис. 1.1. Парусный треугольник.
VA - скорость вымпельного ветра
VТ - скорость истинного ветра
VВ - скорость судна
Каждая сторона треугольника имеет длину и направление, соответствующие названным векторам. Направления векторов заданы углами γ и β. Внутренний угол против стороны Va равен (180° – γ), а так как сумма углов треугольника составляет 180°, угол между векторами VT и VА будет ( γ – β). Рассмотренные несложные построения позволяют вывести полезные зависимости. Согласно теореме синусов отношение стороны треугольника к синусу противолежащего угла является постоянной величиной. Отсюда
VT / sin β = VA / sin (180° – γ) = VВ / sin (γ – β)
| (1.2) |
Для отношения величин вымпельного и истинного ветра получим
VВ / VT = sin (γ – β) / sin β =
(sin γ cos β – cos γ sin β) / sin β = sin γ ctg β – cos γ
| (1.3) |
Величины cos β / sin β = ctg β для различных β показаны на графике (рис. 1.2).
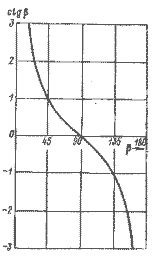
Рис. 1.2. Зависимость ctg β от β.
Выражение (1.3) не содержит приближения, оно является другой формой зависимости (1.1) и справедливо для любого тела, движущегося в воздушной среде. Так как скорость VT и направление у истинного ветра могут быть определены, скорость движения судна зависит от β Чтобы определить физический смысл величины β, обратимся к рассмотрению принципа движения парусного судна.
Вертикальное воздушное крыло (парус) и вертикальное подводное крыло (киль, шверт и т. л.) преобразуют энергию ветра в силу, движущую судно (рис. 1.3).

Рис. 1.3. Идеальное парусное судно.
На практике для уравновешивании направленной вниз силы тяжести необходима эквивалентная сила поддержания — плавучесть. Водоизмещаюший корпус, обладающий необходимой плавучестью, сам по себе не имеет значения для преобразования силы ветра. Система воздушно-подводных крыльев (рис. 1.4,а) подвергается действию сил, показанных на рис. 1.4,б. Поток воды VВ относительно подводного крыла и воздушный поток VА относительно паруса создают силы FH и FA соответственно. При равномерном (без ускорения) движении судна справедливо равенство
FH = FA
| (1.4) |
Гидродинамическая сила FH может быть разложена на две составляющие: силу лобового сопротивления DH, направленную противоположно VВ, и перпендикулярную ей подъемную силу LH (рис. 1.4,в). Отношение этих составляющих (гидродинамическое качество) выражается через угол гидродинамического сопротивления δH = arcctg (LH / D H). Аэродинамическую силу FA можно разложить на пару составляющих — параллельную к перпендикулярную направлению движения судна VB: силу тяги Fx и силу дрейфа Fy. Вторая пара составляющих силы FA, параллельная и перпендикулярная направлению вымпельного ветра VA, представляет собой силу лобового сопротивлении DA и аэродинамическую подъемную силу LA (рис. 1.4, г). Отношение этих последних характеризует аэродинамическое качество или угол аэродинамического сопротивления — δA = arcctg (LA / D A).
Так как сила тяги паруса Fx равна силе лобового сопротивления DH подводного крыла, a Fy = LH, угол между FA и Fy равен δH. Подъемная сила LA перпендикулярна VA, a Fy перпендикулярна VB. Отсюда угол между LA и Fy равен углу между VA и VB и равен
β = δH + δA
| (1.5) |
Это отношение известно под названием теоремы курсов, а выражения
δH = arcctg LH / DH, δA = arcctg LA / DA
| (1.6) |
являются математическим описанием парусного судна. Из уравнения (1.3) видно, что для значений угла γ не слишком близких к 180°, ctg β должен иметь как можно большую величину, чтобы обеспечить возможно большее отношение VВ/VT. Из рис. 1.2 видно, что это соответствует малым углам β. Формулы (1.5) и (1.6) показывают, что это достижимо при высоких значениях отношения подъемной силы к сопротивлению.
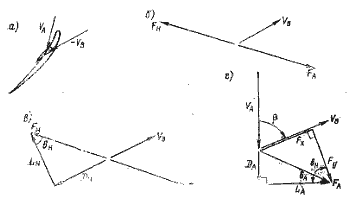
Рис. 1.4. Иллюстрация теоремы курсов.
Итак, определение δH и δA для всех мыслимых значении γ и VT дает исчерпывающее решение проблемы. Для этого необходимо иметь возможность точного вычисления силы сопротивления и подъемной силы для любых VT и γ. Рассмотрим результаты определения величин δH и δA для ряда парусных яхт к попытаемся сделать на этом основании нужные выводы.
На рис. 1.5 приведены значения угла δA для динги 12-футового международного класса, яхты 12-метрового класса и буера в функции курсового угла γ.
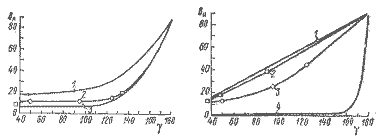 | |
| Рис. 1.5. Угол аэродинамического сопротивления как функция курсового угла относительно истинного ветра: 1 – 12-футовый динги, 2 – яхта 12-метрового класса, 3 – буер. |
Рис. 1.6. Угол гидродинамического сопротивления как функция курсового угла к истинному ветру: 1 – 12-футовый динги, 2 – яхта 12-метрового класса, 3 – катамаран Торнадо, 4 – буер. |
Наибольшее значение δA имеют динги, паруса которых с относительно малым удлинением создают значительное индуктивное сопротивление. У 12-метровиков с высокоэффективными парусами и аэродинамически «чистой» палубой угол аэродинамического сопротивления δA имеет значительно меньшую величину. У буера с жестким парусом это преимущество еще заметнее.
На графике (рис. 1.6) даны значения угла гидродинамического сопротивления δH для тех же судов и катамарана Торнадо. У динги и 12-метровиков они близки по величине. Близкая к линейной зависимость характерна и для других однокорпусных яхт. У Торнадо — типичного быстроходного многокорпусного судна значение δH заметно ниже, у буера оно близко к оптимальному почти на всех курсовых углах.
Для того чтобы приведенные данные отражали реальную физическую картину, построим графическую зависимость суммы углов β = δH + δA от γ (рис. 1.7) и сравним величины отношений VB/VT для рассмотренных судов.
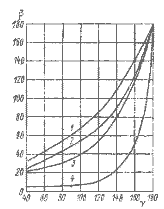
Рис. 1.7. Величина β при различных γ: 1 – 12-футовый динги, 2 – яхта 12-метрового класса, 3 – катамаран Торнадо, 4 – буер.
Полярные, диаграммы для Торнадо, 12-метровика, динги (рис. 1.8) и для буера в сравнении с Торнадо (рис. 1.9) свидетельствуют о том неоспоримом преимуществе по скорости хода, которым обладают многокорпусные парусники по сравнению с классическими яхтами, и о фантастических возможностях буеров, способных при истинном ветре 10 уз развивать скорость 80 уз.
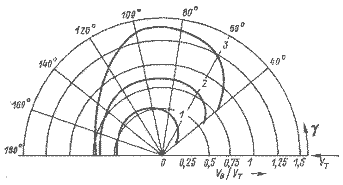
Рис. 1.8. Полярная диаграмма VB/VTпри VT ≈ 10 уз:
1 – 12-футовый динги, 2 – яхта 12-метрового класса, 3 – катамаран Торнадо.
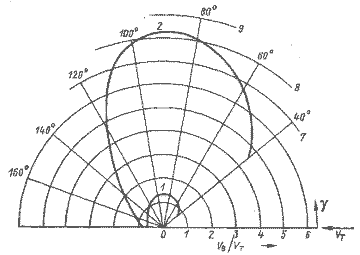
Рис. 1.9. Полярная диаграмма VB/VT при VT ≈ 10 уз:
1 – катамаран Торнадо, 2 – буер.
Фактором, определяющим величину угла аэродинамического сопротивления, является отношение площади паруса к площади парусности судна, не создающей подъемной силы. Для угла гидродинамического сопротивления таким фактором служит отношение площади элементов, создающих сопротивление дрейфу, к площади вертикальной проекции корпуса. В большинстве случаев эти функции не могуг быть четко разделены, так как киль и корпус представляют собой единое целое, что создает большие трудности для аналитической обработки данных. Для конкретного судна названные углы зависят не только от курсового угла γ, но также и от скорости истинного ветра VT. На рис. 1.5 и 1.6 были показаны скорости, развиваемые судами при ветре в 5 — 10 уз. С увеличением скорости ветра в результате крена и необходимости рифить паруса угол аэродинамического сопротивления δA возрастает. Крен и волны аналогичным образом приводят к росту δH. С повышением VT отношение VB/VT уменьшается, как это показано на рис. 1.10, на котором построены поляры для яхты 12-метрового класса при ветре 10 и 20 уз.
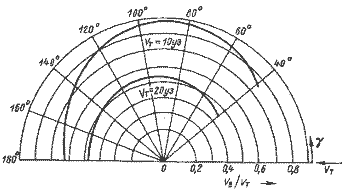
Рис. 1.10. Полярная диаграмма VB/VT для яхты 12-метрового класса.
У идеальной яхты {рис. 1.3) боковая составляющая силы тяги паруса Fy и гидродинамическая подъемная сила киля LH равны, противоположно направлены, а центры их приложения отстоят друг от яруга на величину h (рис. 1.11). Они образуют момент, вызывающий крек судна на подветренный борт.
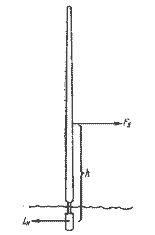
Рис. 1.11. Крепящий момент идеальной яхты.
При крене в результате смещения по горизонтали центра плавучести СВ от центра тяжести судна CG на расстояние Ь возникает откренивающий момент, величина которого возрастает до тех пор, пока не будет равна кренящему моменту.
hFy = bW
| (1.7) |
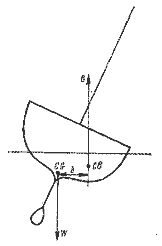
Рис. 1.12. Восстанавливающий момент яхты.
Так как сила Fy, вызывающая крен, пропорциональна площади паруса, то максимальная плошадь парусности пропорциональна произведению Wb/h. Для однокорпусного судна (рис. 1.12) расстояние b ограничено малой шириной корпуса, поэтому сила тяжести W должна быть возможно большей. У яхт 12-метрового класса это условие обеспечивается балластом, размещаемым в нижней части фальшкиля. Восстанавливающий момент динги получается за счет веса команды, которая располагается на наветренном борту.
Многокорпусные яхты, например катамаран (рис. 1.13), относятся к легким небалластируемым судам. Их восстанавливающий момент создается за счет разнесения корпусов и достигает максимальной величины при крене 10°, в то время как у швертбота он соответствует 30°. Таким образом, большая площадь вредного воздушного сопротивления катамарана с избытком компенсируется большей площадью парусности, работающей с большим эффектом благодаря малым углам ходового крена. Под парусами катамараны имеют преимущество в скорости.
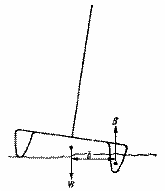
Рис. 1.13. Восстанавливающий момент катамарана.
Многокорпусные парусные суда известны в трех разновидностях: тримарана, проа и катамарана. Тримаран состоит из основного корпуса, поддерживаемого с каждого борта аутригером. Проа имеют два разных по размерам корпуса. Для того чтобы больший корпус был всегда с наветренной стороны, проа при повороте меняет направление движения, поэтому нос и корма имеют идентичные обводи. Катамаран представляет собой два одинаковых корпуса, связанных поперечными балками или мостом; общая ширина судна составляет примерно половину его длины.
В последующих главах принципы конструкции быстроходных парусников рассмотрены детально. При их изучении необходимо помнить приведенные выше критерии, которые обеспечивают достижение высоких скоростей под парусами.
Основное назначение корпуса судна состоит в создании силы плавучести, равной весу судна, экипажа и груза. При движении судно испытывает действие сопротивления R, главную часть которого составляет гидродинамическое сопротивление корпуса Dк. Понимание физической природы сопротивления и средств для его уменьшения является первым условием создания быстроходного парусного судна. К параметрам, которые характеризуют корпус и его движение в зодс, относятся: Vв — скорость судна относительно воды, м/с; W — вес судна с грузом, кг; L — длина ватерлинии, м; В — ширина ватерлинии, м; CF — смоченный периметр наибольшего поперечного сечения подводной части, м.
Сопротивление водоизмещающего (не глиссирующего) корпуса вызывается затратами энергии на преодоление вязкости воды и наличием свободной поверхности на границе воздух — вода. Составляющая трения описывается формулой
RF = ½ pHVB2AFCF
| (2.1) |
где pH — плотность морской воды; AF — смоченная поверхность корпуса; CF — коэффициент трения. Величина последнего определяется взаимодействием сил инерции и вязкости в пограничном слое и выражается как функция числа Рейнольдса
Re = ρHVBL/η
| (2.2) |
где η — динамическая вязкость. Для морской воды, длины судна по ватерлинии L в м и скорости Vв в м/с,
Re ≈ 106VBL
| (2.3) |
На рис. 2.1 показана зависимость коэффициента сопротивления от числа Рейнольдса. При числах Рейнольдса менее 2·105 преобладает ламинарное обтекание и идеальный коэффициент трения (здесь под идеальным коэффициентом трения понимается коэффициент трения эквивалентной пластины, т. е пластины. движущейся со скоростью судна и имеющей равную с ним длину по ватерлинии и площадь смоченной поверхности — прим. научн. ред.) определяется формулой Блазиуса
CF = 1,328/Re½
| (2.4) |
Между значениями Re = 2·105 и Re = 1,5·106 (заштрихованный участок на графике) ламинарное обтекание переходит и турбулентное. В переходной зоне наблюдаются значительные колебания CF.
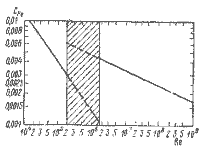
Рис. 2.1. Коэффициент трения в зависимости от числа Рейнольдса.
Когда число Рейнольдса больше 1,5·106, устанавливается турбулентное обтекание. Для определения коэффициента трения в этом случае используется формула Прандтля — Шлихтинга
CF = 0,455 / (lgRe)2,58
| (2.5) |
Эта формула удовлетворяется при условии, что произведение VBL больше 12, и пригодна для всех рассматриваемых размерений судов и скоростей. Теоретически полученный коэффициент CF нуждается в некоторых уточнениях перед его использованием в формуле (2.1).
Для реальных корпусов с учетом неизбежных срывов потока у кормы приемлема эмпирическая формула
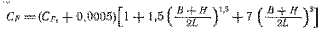
| (2.6) |
Другая составляющая сопротивления — волновое сопротивление качественно может быть описано следующим образом. Согласно закону Бернулли ξ — подъем воды вдоль корпуса относительно статической ватерлинии и скорость V потока за кормой должны удовлетворять отношению
V2 + 2gξ = VB2
| (2.6) |
где g = 9,81 м/с2 — ускорение силы тяжести. У форштевня поток воды притормаживается (следовательно, ξ>0), затем у мидель-шпангоута скорость его возрастает до величины несколько большей скорости VB движения судна ξ< 0) и вновь падает у кормы (ξ>0), где поток сливается с кильватерной струей. Такова модель возникновения носовых и кормовых расходящихся волн, в дополнение к которым из-за вертикальных перемещений воды образуются поперечные волны. Скорость движения волны VW на глубокой воде пропорциональна корню квадратному ее длины λ. Так как волны должны двигаться вместе с судном, получаем
VB = VW = (λg/2π)½
| (2.8) |
т. е. длина волны возрастает пропорционально квадрату скорости судна. Эта зависимость показана на рис. 2.2.

Рис. 2.2. Волнообразование при различных относительных скоростях судна.
Если учитывается ограниченная глубина d, то VB = (λg/2π)½· (th2πd/λ)½, а для d значительно меньшей λ имеется тенденция к VB = gd½ . Прн этой скорости на мелководье начинает сказываться трение воды о дно водоема. На рис. 2.2 показаны спстемы волн для ряда скоростей VB. С учетом формулы (2.8) можно выразить скорость судна в безразмерном виде как отношение длины волны λ к длине судна L
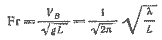
| (2.9) |
где Fr — число Фруда. Морские инженеры часто представляют число Фруда в иной форме, как скорость в узлах, отнесенную к корню квадратному из длины судна в футах. Эта характеристика, получившая название отношения скорости к длине (SLR) связана с числом Fr равенством SLR/Fr = 3,36. При длине волны от λ ≈ L до λ = (3—4)L склон ее располагается таким образом, что судно как бы все время должно подниматься в гору. Если описать профиль носовой волны выражением
ξ = cos kx
| (2.10) |
где
k = 2π / λ = g / VB½
| (2.11) |
то наклон волны будет ξ k sin kx, а его средняя величина для судна длиной L
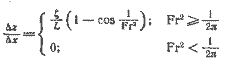
| (2.12) |
Волновое сопротивление представляет собой составляющую силы тяжести, направленную вдоль переднего склона волны W sin θ (Здесь aвтop пользуется очень упрощенным понятием о волновом сопротивлении. которое в достаточно общем случае можно определить как сопротивление, обусловленное затратами энергии на образование волн. — Прим. науч. ред.) или при малом подъеме волны для узких корпусов W tg θ = W (Δz / Δx). Таким образом,
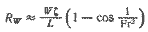
| (2.13) |
Подобное выражение, полученное я проверенное экспериментально П. Мейсоном, дает хорошие результаты при расчетах сопротивления однокорпусных судов.
Можно приближенно оценить величину ξ — амплитуду носовой волны следующим образом. Вода отбрасывается от бортов судна на расстояние, пропорциональное В, в течение времени соразмерного L / VB. Средняя скорость перемещения воды составит величину порядка VB(B / L). Приравнивая соответствующие количества кинетической (W / 2g) VB2 (B / L) и потенциальной (W / g) g ξ энергии, находим
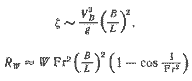
| (2.14) следовательно, (2.15) |
представляет собой формулу первого приближения для вычисления волнового сопротивления. Этого, однако, недостаточно.
Точная теория была предложена в 1932 г. Хавелоком. В упрощенном общем виде формула Хавелока была представлена Кестлом для корпусов, обладающих продольной и поперечной симметрией. Выражение, предложенное Кестлом для однокорпусных судов, имеет вид
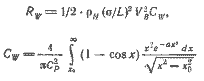
| (2.16) где (2.17) |
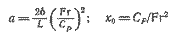
| (2.18) |
Величина δ — заглубление центра тяжести наибольшего поперечного сечения площади б. Призматический коэффициент
CP = W / ρHgσL
| (2.19) |
(Эквивалентом призматического коэффициента в отечественной литературе является коэффициент продольной полноты, равный отношению объемного водоизмещения к произведению площади мидель-шпангоута на длину судна. — Прим. науч. ред.)
характеризует распределение площади поперечных сечений по длине судна.
Волновое. сопротивление более илн менее нечувствительно к форме поперечного сечения корпуса. Напротив, сопротивление трения непосредственным образом зависит or смоченной поверхности AW. Величина AW с достаточно высокой точностью (±1%) для широкого ряда форм выражается формулой
AW = 0,74GmL
| (2.20) |
Минимальный периметр поперечного сечения заданной площади имеют полукруглые корпуса, для которых Gm = 1/2πВ и AW = 1.16 ВL. Так как волновое сопротивление не зависит от формы поперечного сечения, можно ограничиться рассмотрением полукруглых обводов. В этом случае б=πВ2/8, δ = В/π и общее сопротивление может быть представлено а зависимости от числа Фруда Fr, отношения длины корпуса к ширине L/B и призматического коэффициента GF
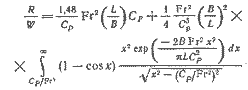
(2.21) |
Одной из первых величии, которую нужно выбрать, проектируя судно, является отношение водоизмещения к длине судна DLR = Δ / (0,01L)3, где Δ — водоизмещение а «длинных тоннах» (единица массы, используемая в Великобритании — прим. науч. ред. Δ = 1016 кг= 2240 ф). Используя формулу (2.19), найдем для корпусов с полукруглыми поперечными обводами
DLR = 11200 CF (B/L)2
| (2.22) |
При разработке проекта одно ограничение вызывается отношением прочности материала к его весу, другое — необходимостью сделать DLR минимальным. Из выражения (2.22) видно, что одно и то же DLR может быть получено для бесконечного ряда величин CF и L/В. Необходимо подобрать эти величины так, чтобы получить минимальное сопротивление. Обе составляющие сопротивления — сопротивление трения и волновое — увеличиваются с ростом Fr2, однако выражение для волнового сопротивления включает дополнительную функцию от квадрата числа Фруда, которая бесконечно мала для очень малых или очень высоких значений Fr2 и достигает максимальной величины при Fr2 = 0,281 (VB / L½ ≈ 1,78). Целесообразно сравнивать сопротивления судов, имеющих это или чуть большее значение Fr. Используя уравнение (2.21), вычислим величину R/W для корпусов с призматическим коэффициентом от 0,5 до 0,8 к отношением L/B от 8 до 32 при фиксированной величине Fr2 = 0.355 (VB / L½ = 2) Результаты представлены на рис. 2.3.
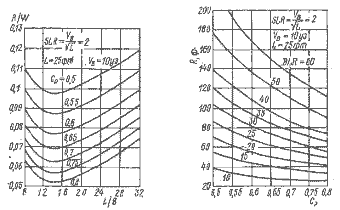 | ||
| Рис. 2.3. Зависимость сопротивления воды движению судна от величины L/D при VB / L½ = 2 |
Рис. 2.4. Зависимость сопротивления воды движению судна от CF при VB / L½ = 2 | |
Лучший результат получен для корпусов с большим CF и отношением L/B от 12 до 16. Для расчета сопротивления трения была задана длина корпуса 7,6 м, но учитывая, что приведенные на графике результаты мало зависят от абсолютных размеров, можно считать, что эти кривые имеют общий характер.
График рис. 2.3 все же не дает ответа на главный вопрос: какова величина призматического коэффициента необходимая для того, чтобы для заданных веса и длины (DLR) сопротивление R (а не отношение R/W) было бы минимальным? Перестроим трафик (рис. 2.4) и увидим, что высокие значения призматического коэффициента предпочтительны; подразумевается, что это справедливо даже для CF > 0,8. Выбор призматического коэффициента легче осуществить при малых значениях DLR. Чтобы должным образом оценить данные рис. 2.4. следует помнить, что образование вихрей к срыв потока при обтекании выступающих частей и корпуса не учтены. Для высоких значений CF корпус по обводам приближается к скоу (большая плоскодонная лодка с прямоугольными оконечностями, шаланда — прим. научн. ред). и следует ожидать разрыва сплошности потока у носовой оконечности. В результате сопротивление при таких экстремальных CF будет иметь тенденцию к возрастанию. Отсюда следует, что оптимальная величина CF для судов с малым значением DLR лежит в пределах 0,65 — 0,75.
Рассмотрим некоторые варианты обводов, для которых полученные выше результаты могут измениться. Смещение максимальной площади поперечного сечения в нос от миделя приводит к увеличению сопротивления при любой скорости. Напротив, сдвиг наибольшего поперечного сечения в корму может снизить величину R/W примерно на 5% для L/B = 12 при отношении скорости к длине (SLR) от 0.8 до 3. Вне этого диапазона скоростей симметричные в обоих направлениях от миделя корпуса имеют преимущество. Чувствительность R/W к положению наибольшего поперечного сечения по длине судна уменьшается с. увеличением L/В и CF. Для высоких значений этих величин положение наибольшего поперечного сечения интересующих нас корпусов в большей мере определяются конструктивными соображениями, чем уменьшением сопротивления.
Другой возможностью модификации обводов является расширение и уплощение кормовой части. Достигаемый при этом эффект, оказывающий влияние из R/W, по величине и зависимости от DLR имеет тот же характер, что и от смещения по длине наибольшего сечения в корму, а .плоские кормовые обводы не дают положительного результата при SLR менее 0,8 и более 3. Это изменение обводов приводит к усилению демпфирования килевой качки (подробнее этот вопрос рассматривается в гл. б). У корпусов с низким DLR гашение килевой качки не требует уплощения кормовой оконечности.
Для того чтобы перейти к рассмотрению многокорпусных судов, введем некоторые рабочие определения. Будем называть корпус, в котором размещается груз (в том числе экипаж), корпусом, а обеспечивающие остойчивость поплавки – аутригерами. В общем случае поплавки должны быть как можно более легкими.
Катамараны состоят из двух идентичных или (при несимметричных обводах), расположенных зеркально, корпусов. Катамараны в пределах размерений прогулочного судна быстроходнее тримаранов благодаря уменьшению сопротивления при выходе наветренного корпуса из воды и эффективной работе парусов за счет малого ходового крена. Плавание с одним корпусом над водой будет рассмотрено в гл. 4. Для плавания при небольшой волне предпочтительны корпуса катамаранов с полукруглыми обводами на большей части длины, несколько уплощенные в корме (на трети длины) и переходящие в эллиптическую, параболическую и V-образную форму в носу.
При наличии волн длиной более длины судна сопротивление однокорпусных яхт на острых к ветру курсах значительно возрастает. Оно уменьшается с увеличением отношения L/B к остается практически неизменным для различных отношении В/Н. Отсюда вытекает, что оптимальное сечение корпуса для катамарана открытою моря будет соответствовать значению В/Н, несколько меньшему, чем у полукруглых корпусов, у которых В/Н = 2. На большой скорости наветренный корпус, оторвавшись от поверхности воды, будет испытывать сильные удары о золны. Чтобы уменьшить силу этих ударов, полукруглые обводи заменяют скругленными, М-образными или параболическими.
Вопрос о преимуществах симметричных кли асимметричных обводов катамарана не имеет однозначного ответа. Главным преимуществом асимметричных обводов считается повышение горизонтальной подъемной силы на более выпуклом борту. При расположении выпуклых бортов с внутренней стороны катамарана горизонтальная подъемная сила, создаваемая ими, будет только сжимать поперечные связи, не считая положения, при котором наветренный корпус выйдет из воды (рис. 2.5).
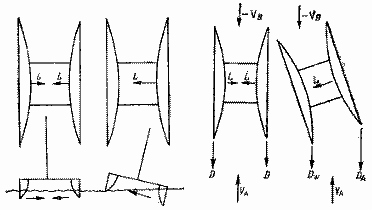 | ||
| Рис. 2.5. Роль асимметрии обводов в создании поперечной силы. | Рис. 2.6. Влияние асимметричных обводов на устойчивость движения катамарана. | |
С таким креном непродолжительное время могут ходить только небольшие суда. Применение асимметричных обводов вызывает также возражения в связи с тем, что для длинных мелкосидящих корпусов заметное увеличение горизонтальной подъемной силы достижимо при углах атаки >10°. Такой угол между диаметральной плоскостью и курсовой линией при движении судна приводит к столь значительному увеличению сопротивления воды, что нет смысла и рассматривать вопрос.
Асимметричные корпуса, однако, обеспечивают повышенное сопротивление рыскливости судна при плавании на волнении. При отклонении судна от курса примерно на 10° горизонтальная подъемная сила Dk подветренного корпуса значительно возрастает (рис. 2.6) и сопровождается повышением индуктивного сопротивления. Наветренный корпус имеет отрицательный угол атаки и не создает заметной подъемной силы DW. Избыток сопротивления на подветренном корпусе но сравнению с наветренным создает момент, противостоящий уходу с курса. Принимая решение о применении асимметричных обводов, необходимо учитывать, что для корпусов с отношением В/Н = 1.5 произойдет 5%-ное увеличение смоченной поверхности и, следовательно, повышение сопротивления. Сопротивление трения преобладает в общем балансе сопротивления при плавании в слабый ветер (многокорпусные суда в этих условиях вообще малоэффективны) и при высоких скоростях (SLR >= 2,8).
Еще одно соображение по поводу обводов корпусов: из двух видов кормовых образований — транцевого и заостренного, типа каноэ, предпочтение можно отдать второму. Транцевые корпуса обладает большим сопротивлением формы при малых скоростях (SLR <= 2,8). Давление воды на корпус в носовой от мидель-шпангоута части, создающее сопротивление, при острой кормовой оконечности компенсируется в значительной мере давлением воды на корпус позади мидель-шпангоута, что не обеспечивается при полных кормовых образованиях. При больших скоростях (SLR >= 2,8) разница в сопротивлении транцевых и острых с кормы корпусов небольшая – (незначительное преимущество дают полные кормовые образования). Для гоночных яхт открытого моря надо учитывать, что в свежий ветер корма нередко оказывается под водой. В этих условиях сопротивление от встречных волн меньше при острой корме.
Применительно к тримаранам проблема выглядит иначе. Так как весовая нагрузка сосредоточена в главном (среднем) корпусе. для его обводов предпочтительны полукруглые сечения на большей части длины. К корме сечения могут быть более плоскими. в носу —-заостренными. Отношение DLR для корпуса тримарана более чем вдвое превышает эту величину для каждого корпуса катамарана тех же размерений, поэтому есть смысл использовать транцевую корму.
Конструкция аутригеров тримарана, как к их положение относительно среднего корпуса, требуют специальною рассмотрения. Существуют два подхода к выбору объема аутригеров. Согласно первому поплавок должен выдерживать полный вес судна, не погружаясь под воду; сообразно второму он рассчитывается на полное погружение при предельных ветровых нагрузках. Вопрос выяснился после серии опрокидываний тримаранов с малообъемными аутригерами в 1976—1977 гг. Оказывается, в штормовых условиях с убранными парусами тримаран может получить на волне крен, из-за которого подветренный аутригер малого объема уже не будет в состоянии обеспечить боковую остойчивость. Имея большое боковое сопротивление, аутригер играет роль фиксированной оси поворота, вокруг которой происходит опрокидывание. Можно сказать, что выбор полно- или малообъемного аутригера зависит от решения вопроса, какой характер опрокидывания судна представляет большую опасность: на волне без парусов или на ходу под полными парусами.
Для быстроходных тримаранов предпочтительнее аутригеры с полукруглыми обводами на длине более 70%, переходящие в заостренные к форштевню. Носовые обводы корпуса и аутригеров тримарана выбираются с таким расчетом, чтобы при встрече с небольшой волной они легко рассекали ее и обладали в то же время хорошей всхожестью на крупную волну, исключающей зарывание в воду с последующей возможностью опрокидывания по диагонали или через оконечности. На этих основаниях носовые обводы делают достаточно острыми с умеренным свесом, кривизной и развалом бортов (последнее касается только аутригеров). Аутригеры могут снабжаться волноотбойными плитами (рис. 2.7).

Рис. 2.7. Средства улучшения всхожести аутригера на волну:
подъем носовой оконечности и плиты-брызгоотбойники.
На острых к ветру курсах глубоко погруженный подветренный аутригер испытывает значительное боковое сопротивление, которое создает момент, уваливающий судно под ветер. Чтобы уменьшить этот неблагоприятный эффект, аутригеры устанавливают так, чтобы цевтр бокового сопротивления лежал па 8 – 15% (в зависимости от общей ширины судна) ближе к носу, чем у корпуса (рис. 2.8).
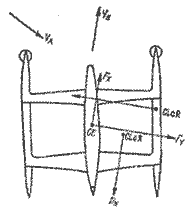
Рис. 2.8. Баланс моментов рыскания при ходе тримарана на ветер.
Аутригеры устанавливают обычно так, чтобы при средней нагрузке и положении судна на ровный киль они не касались воды. На попутных курсах это дает тримарану по сравнению с катамараном выигрыш в сопротивлении. На крутых курсах тримаран ходит с большим креном, чем катамаран.
Подветренный поплавок при этом должен подниматься над водой так, чтобы ло возможности не подвергаться ударам волн. С учетом угла дрейфа λ поплавки разворачиваются под эквивалентным углом в диаметральной плоскости судна, что позволяет снизить лобовое сопротивление воды. Принято также устанавливать аутригеры под углом примерно 15° к вертикальной плоскости, что дает возможность уменьшить нагрузку на поперечные связи, а глазное — понизить лобовое сопротивление, так как на крене аутригер оказывается и положении на ровный киль.
Чтобы не допустить резкого увеличения сопротивления при полном погружении аутригера в соду, его DLR должно быть возможно меньшим. Поэтому резервный объем аутригера необходимо обеспечить за счет его удлинения, учитывая отношение веса конструкции к ее прочности. В сложившейся практике (по данным на 1977 г.) более 80% тримаранов строится с аутригерами, по длине равными корпусу, но не исключено применение аутригеров и с большей длиной.
Проа представляет собой менее изученный тип многокорпусного судна. Микронезийское проа состояло из узкого асимметричного подветренного корпуса и тяжелого аутригера (балансира), расположенного с наветренной стороны. Судно управлялось большим, физически сильным экипажем, который размещался на аутригере, откренивая своим весом проа так, чтобы поплавок скользил у самой воды, не касаясь ее поверхности.
Немногочисленные современные суда этого типа, рассчитанные на плавание в открытом море и получившие название "атлантических проа", имеют, в отличие от микронезийского прототипа, основной наветренный корпус, а аутригеры с малой плавучестью размещены с подветренной стороны. Исключение представляет собой Чирс конструкции Ньюика — проа с парусным вооружением шхуны с аутригером, по объему равным основному корпусу. Нагляднее можно представить проа атлантического типа в виде тримарана с отрезанными наветренным поплавком и поддерживающей его поперечной связью. Микронезийский аутригер (балансир) стал корпусом, а микронезийский корпус — полностью погружающимся при крене аутригером. Продольные обводы проа имеют конфигурацию двух соединенных вместе передних (от мидель-шпангоута) частей корпуса тримарана.
Сравнивая ходовые качества проа и катамарана, выясняем, что для судов небольших размеров концентрация экипажа на наветренном борту дает катамарану все преимущества проа. У более крупных судов, для которых перемещение экипажа не имеет существенного значения, конструкция проа предпочтительнее. так как при этом обеспечивается постоянное смещение нагрузки к наветренной стороне. По сравнению с тримаранами важными преимуществами проа являются меньшие вес и воздушное сопротивление, получаемые благодаря отсутствию второго аутригера. Выигрыш в весе может быть использован для укрепления и удлинения поперечных связей и, благодаря этому, дополнительного смещения центра тяжести на ветер. В открытом море проа по ходовым качествам превосходят катамараны и тримараны ка любых курсах. Тримараны быстроходнее катамаранов на попутных курсах и в слабый ветер, когда сопротивление аутригеров может быть сведено до минимума или полностью исключено. Следует отметить, что разница в ходовых качествах этих судов гораздо меньше, чем преимущества, которые имеют по сравнению с ними проа.
На основании уравнения (2.21) и пропорциональности сопротивления величине WFr2 можно предположить, что многокорпусные суда, имеющие относительно низкое значение DI.R, будут удовлетворять условиям упрощенной формулы сопротивления
R / W = a Fr2
| (2.23) |
где а — близка к постоянной величине. Это вполне соответствует действительности. В отчете симпозиума по скоростным парусным судам, проведенного Королевским парусным союзом, Д. Келсел представил данные по испытаниям в опытовом бассейне 5-футовой модели тримарана и результаты расчетов сопротивления нескольких многокорпусных судов по формулам международных правил для многокорпусных судов открытого моря (IOMR). В обоих случаях были получены плавные параболические кривые, соответствующее уравнению (2.23). где постоянная а изменялась в пределах 0.025—0.032. Примечательно, что Келсел не обнаружил на кривой горбов, отражавших волновое сопротивление, как это можно видеть у однокорпусных яхт.
Перейдем к рассмотрению планировки многокорпусных судов. Минимальные требования предусматривают наличие спального места для каждого члена экипажа, гальюна, камбуза, некоторого количества полок и ящиков для припасов, штурманского стола и т. п. Рассмотрение вариантов общего расположения и оборудования выходит за круг вопросов, которым посвящена книга. Ограничимся соображениями общего плана.
Как об этом говорилось, ширина корпуса по ватерлинии должна быть возможно меньшей; однако выше ватерлинии борта имеют развал либо выступы, за счет чего койки, ящики, полки размещаются, оставляя достаточно свободного места для прохода.
На катамаранах, как правило, все помещения располагают на мостике, так как корпуса слишком узки. Вследствие этого повышается центр тяжести, увеличивается аэродинамическое сопротивление корпуса судна. В какой-то мере снизить значение этих неблагоприятных факторов удается, используя в качестве элементов поперечных связей детали оборудования.
У тримаранов и проа помещения сосредоточены в главном корпусе. У проа, имеющего симметричные относительно миделя обводы, кокпит расположен в средней части, у тримарана — в корме. Во всем остальном планировка этих судов мало различается. Следует избегать размещения грузов в оконечностях, чтобы уменьшить момент инерции килевой качки и тем самым снизить ее амплитуду. Это важно для снижения сопротивления от морского волнения.
Таким образом, обитаемой остается только средняя часть корпуса. Часто пространства в корпусе, которые нежелательно (и невозможно) использовать для размещения грузов, заполняют пенопластом. При этом нельзя забывать, что он не только заполняет объем, но и увеличивает вес корпуса. Далеко не всегда на судне малых размеров имеет смысл оборудовать рубку выше палубы. Лучше продлить линию погиба бимсов аутригеров н оборудовать сплошную палубу по всей ширине судна. В корме и в носу от миделя линия борта будет плавно примыкать к этой палубе, исключая плоские поверхности, нерациональные со всех точек зрения (по соображениям прочности, аэродинамики, эстетики). Удачным примером подобной конструкции может служить тримаран Три Чирс (рис. 2.9), построенный по проекту Д. Ньюика.
Из сказанного ранее следует, что достижение высоких скоростей под парусом во многом зависит от того, насколько удается облегчить судно. Корпусные конструкции должны выдерживать пики напряжений, но не за счет применения сверхмощных связей. Основные нагрузки, испытываемые одномачтовой яхтой, показаны на рис. 3.1, где Т — растяжение, С — сжатие.
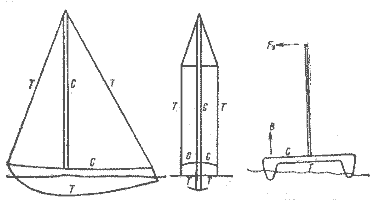 | ||
| Рис. 3.1. Напряжения, испытываемые корпусом и оснасткой яхты. | Рис. 3.2. Напряжения, испытываемые поперечными связями катамарана при наличии крена. | |
Чтобы паруса работали эффективно, такелаж, а вместе с ним и все прочие конструкции должны обладать большой жесткостью. Этот вывод в полной мере относится и к многокорпусным судам, для которых рассматриваемый вопрос имеет особую важность.
У тримаранов, чьи мачты устанавливаются в диаметральной плоскости главного корпуса, распределение нагрузок в продольном направлении имеет тот же вид, что и у однокорпусных судов. Ванты нередко крепятся к аутригерам, что дает возможность упростить их проводку, отказавшись от применения краспиц и ромбовант. В этих случаях поперечные связи аутригеров испытывают действие значительного изгибающего момента. Необходимо, чтобы они обладали достаточной жесткостью для ограничения изгиба мачты. На катамаранах мачта опирается на соединяющие корпуса поперечные связи, которые, помимо других нагрузок, должны выдерживать ее сосредоточенное давление. Поэтому для многокорпусных судов следует установку парусного вооружения увязывать с конструктивными элементами так, чтобы по возможности избегать высоких напряжений в стоячем такелаже. Детально эта рекомендация рассматривается далее.
Для удовлетворения требований прочности главное внимание должно быть обращено на конструкцию поперечных связей, соединяющих корпуса. Па рис. 3.2 изображена схема катамарана. идущего с креном. При изгибе поперечной балки под действием силы плавучести, приложенной к подветренному корпусу и направленной вверх, верхний пояс балки испытывает сжатие, а нижний — растяжение. В предельном случае, когда наветренный корпус целиком выходит из зоды, а сила плавучести подветренного корпуса равна весу судна, максимальное напряжение в балке определяется формулой
σmax = Wlh / I
| (3.1) |
где l — длина поперечной связи, равная расстоянию между диаметральными плоскостями корпусов, h —половина высоты сечения балки, I - момент инерции, зависящий от формы поперечного сечения. Для сплошной балки прямоугольного сечения шириной а и половиной высоты h
I = 2/3 · ah3
| (3.2) |
а для подобной пустотелой балки с толщиной стенок t (см. рис. 3.3)
I = 2/3 · a[h3 – (h – t)3]
| (3.3) |
Для сплошной балки круглого сечения радиусом г
I = π / 4 · r4
| (3.4) |
а для аналогичной пустотелой балки
I = π / 4 · [r4 – (r – t)4]
| (3.5) |
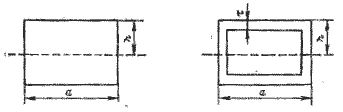
Рис. 3.3. Сечение поперечной балки катамарана.
Для судов, имеющих шверты или кили, поперечные связи испытывают сжатие (рис. 3.4).
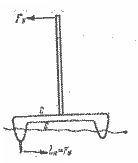
Рис. 3.4. Сжимающие усилия в поперечных связях катамарана на курсе бейдевинд.
Если считать, что максимальная поперечная аэродинамическая сила Fy по величине близка к весу судна W, то напряжение сжатия выразится уравнением
бmax = W / A
| (3.5) |
где А — половина площади поперечного сечения балки, т. е. A = hа — для сплошной и A = 2t (h+a) для пустотелой балки прямоугольного сечения.
Наконец, мы имеем дело с напряжениями среза н скручивания, возникающими в результате килевой качки корпусов. На рнс. 3.5 показана схема возникновения этих усилий при постановке одного корпуса кормой, а другого носом на вершину волны, или, условно, на жесткие опоры.
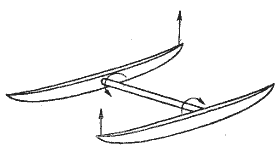
Рис. 3.5. Скручивающие усилия в поперечной связи катамарана при косой постановке на волну.
Такая ситуация, в принципе возможная при плавании в открытом море, представляется наиболее опасной. Крутящий момент, приложенный к поперечной балке, ранен приблизительно 1/2 WL, где W — вес судна, L — его длина. Этот момент приводит к скручиванию сечений балки на угол ϕ, равный
ϕ = WLl / 2GIP
| (3.7) |
где G — модуль упругости при сдвиге, IP – полярный момент инерции для сплошной балки круглого течения равен 1/4 π r4. Энергия, соответствующая такой упругой деформации, определится формулой
e = W2 L2 G3 / 2 IPl
| (3.8) |
Она имеет значительную величину и сказывается на ходкости судна По этой и другим причинам следует избегать применения гибких связей корпусов. Исследуя формулу (3.8), легко убедиться, что единственная величина, которая поддается контролю, эго момент инерции IP.
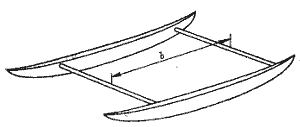
Рис. 3.6. Двухбалочная поперечная связь корпусов катамарана.
Для системы, состоящей из двух поперечных балок (рнс. 3.6), полярный момент инерции пропорционален b3r, что значительно превышает его величину для одной связи. Максимальное срезывающее напряжение в каждой балке будет порядка
бmax = 4W2 Lr / π b4
| (3.9) |
которое при достаточно большой величине b не создаст проблем для обеспечения прочности.
Для того чтобы из приведенного анализа получать практические рекомендации, примем вполне допустимые приближения: r ≈ 0,1l; b ≈ l; L ≈ 21. Тогда изгибающие, сжимающие и скручивающие напряжения, заданные уравнениями (3.1). (3.6) и (39), находятся в соотношении: 4000:100:0.8. Таким образом, если конструкция рассчитана на изгиб, то сжатие для нес нс представляет опасности. Еще меньшая величина напряжения кручения может, однако, ввести в заблуждение. Она не представляет угрозы для самих балок, но может вызвать концентрацию напряжений в месте их соединения с корпусами. Идеальным конструктивным решением с учетом такой возможности следует считать крепление оконечностей балок между двумя переборками в корпусе.
На гоночных судах в качестве поперечных балок используются более сложные конструкции (рис. 3.7,а).

Рис. 3.7. Поперечные связи тримарана, выполненные в виде ферм.
Подобные связи способны выдерживать большие удельные нагрузки на единицу веса, однако верхний их пояс подвергается сжатию, в десять пятнадцать раз превышающему вес судна. Чтобы предотвратить опасный изгиб, необходимо вертикальными распорками соединить верхний пояс с нижним (рис. 3.7.6). Такие арочные конструкции поперечных связей различного сечения, соединяющиеся с поставленными наклонно поплавками, дают лучшее решение задачи. Нецелесообразно для повышения прочности использовать дополнительную, третью связь, устанавливаемую между двумя названными, так как величина отношения прочности к весу при атом снижается.
Остановимся на вопросе оценки конструкционных материалов. Для многокорпусных парусников их выбор ограничивается фанерой, армированными пластинами и легкими сплавами. Характеристики этих материалов приведены в табл. 3.1.
(Внимание! В связи с сомнительностью ряда данных таблица из книги заменена на аналогичную, но приведены лишь условные величины. Механические характеристики зависят от вида нагрузки (изгиб, сжатие, растяжение), а для волокнистых материалов и от направления нагрузки по отношению к направлению волокон. Для реальных расчетов ищите необходимые данные самостоятельно. — Прим. ГШ)
Таблица 3.1. Характеристики некоторых судостроительных материалов
| Наименование | Плотность, г/см3 | Предельное напряжение кГ/мм2 | Модуль Юнга, ГПа2 |
|---|---|---|---|
| Сталь | 7.8 | 32 | 200 |
| Красное дерево | 0,75 | 7,4 | 10 |
| Алюминиевые сплавы | 2,7 | 21 | 71 |
| Стеклопластик | 1,6 | 12 | 55 |
| Углепластик | 1,5 | 90 | 145 |
Деревянные конструкции за последние годы стали шире применяться благодаря использованию эпоксидных смол. Шпоновые конструкции высокой водостойкости позволили удвоить, по сравнению с незащищенным от намокания деревом, предельно допустимые напряжения на изгиб н сжатие. Появилась возможность строить легкие и прочные суда при сравнительно невысоких затратах на материал. Холодная формовка требует высоких затрат ручного труда, поэтому малопригодна для серийного производства. Этим методом, в основном, пользуются любители, которые строят довольно удачные суда.
Другим перспективным путем использования древесных материалов являются сэндвичевые конструкции. Балка из двух поясов красного дерева с вклеенным между ними на эпоксидном клее заполнителем из бальзового дерева при равной прочности па изгиб вдвое легче цельного бруса из красного дерева того же сечения. Такие пояса имеют слабое сопротивление ударным нагрузкам. Этот недостаток может быть устранен, если оклеить их стеклотканью.
Сталь — малоподходящий материал как для многокорпусных, так и для обычных яхт, если их размеры не превышают 30 м. Сварочные деформации, необходимый запас на коррозию ограничивают минимальную толщину стального листа, пригодного для обшивки корпуса, 4-5 мм. Это ограничение несущественно для обшивки из алюминиевых сплавов, которые к тому же не нуждаются в окраске, так как образующиеся на них окислы инертны и служат надежной защитой от коррозии. Следует учитывать опасность электролитической коррозии при швартовке к металлическим пирсам или, что еще хуже, к деревянным судам, обшитым медными листами.
Кроме того, сварка легких сплавов должна выполняться в среде инертных газов, вследствие чего этот метод не применяется в любительском судостроении. Применение таких высокопрочных материалов, как углепластик, сэндвичевые конструкции с пенополиуретановыми заполнителями позволяет создавать легкие, прочные и жесткие конструкции. Более того, эти материалы гораздо проще в обработке, чем даже дерево, и, в принципе, могут использоваться при любительской постройке судна. Необходимую прочность на растяжение можно получить при весьма тонких наружных слоях. Единственным аргументом в пользу применения более толстых оболочек является склонность пластмасс к старению. Полистироловые и эпоксидные смолы под действием ультрафиолетовых лучей разрушаются, на поверхности покрытия образуются волосные трещины, которые постепенно углубляются. В результате сильных ударов о волны период эксплуатации корпуса океанского гоночного катера, сформованного из материала с очень тонким покрытием, обычно бывает немногим более года. Если строить многокорпусные гоночные суда, рассчитанные на столь же непродолжительное время, то похожие тонкие оболочки вполне пригодны.
Сэндвичевые конструкции используются для таких тяжело нагружаемых деталей, как шверт и руль. В этих случаях применяются оболочки, заполненные пенопластовым наполнителем, подкрепленные уложенными волнообразно прядями стекловолокна (рис. 3.8).

Рис. 3.8. Сэндвичевая конструкция пера руля (стеклоткань и пенопласт).
Для прочности внешнюю оболочку делают из углепластика. Кроме того, для компенсации местных нагрузок, например у выхода шверта из швертового колодца, толщину оболочки и армирующих слоев стеклоткани увеличивают.
Из армированного стеклопластика делают мачты и другие детали рангоута. Из такого материала Д. Ньюик изготовил 11-метровую мачту для проа, которая имела у шпора диаметр 152 мм, уменьшающийся к топу до 62 мм. Для ее изготовления использовались сверхпрочные графитовые нити на эпоксидной смоле. Вес мачты составил 29,5 кг. Ее сделали из двух частей, соединенных с помощью втулок и закрепленных самонарезающимися шурупами. Полную парусность 19 м2 мачта выдержала в очень свежий ветер, когда собственная скорость проа достигала 20 уз.
Cила ветра, действующая на парус, выражается формулой
FA = 1/2 · ρAVA2ASCA
| (4.1) |
pA — массовая плотность воздуха на уровне моря (при 20°C ρA = 1,20 кг/м3),VA —скорость вымпельного ветра. AS — площадь паруса, CL — численный коэффициент. Как было показано в гл. I, эта сила может быть разложена на подъемную силу
FA = 1/2 · ρAVA2ASCL
| (4.2) |
FA = 1/2 · ρAVA2ASCD
| (4.3) |
так что
FA = (LA2) + DA2) ½
| (4.4) |
Коэффициент подъемной силы CL имеет почти линейную зависимость от угла атаки α вплоть до его критического значения, а также зависит от удлинения паруса, величину которого определяют по формуле
A = S2 / AS
| (4.5) |
В этом выражении S — размах паруса, равный его высоте. Если нижняя шкаторина расположена близко от палубы или имеет «шайбу» (так называется плита, устанавливаемая на боковых кромках крыла для того, чтобы исключить перетекание воздуха, — прим. перев.), эффективность паруса возрастает, как если бы его относительное удлинение удвоилось. Например, если передняя шкаторина треугольного паруса длиннее нижней в полтора раза, то его удлинение — А = 3, с шайбой оно может быть принято до А = 6 (в зависимости от эффективности шайбы). Можно еще более повысить условную величину относительного удлинения, установив шайбу также по верху паруса, однако конструктивно это трудно выполнить. В зависимости от А и аr — угла атаки, измеренного (в градусах) от угла нулевой подъемной силы, величина коэффициента подъемной силы приближенно определится выражением
CL ≈ 0,11 аr A / (A + 2)
| (4.6) |
Определение аэродинамического сопротивления — значительно более сложная задача. В дополнение к сопротивлению паруса имеет место вредное сопротивление корпуса судна, надстройки н т. п. По этой причине общее лобовое сопротивление находят практическим путем, испытывая модель судна в аэродинамической трубе. С помощью пружинного динамометра замеряют аэродинамическое сопротивление натурного судна.
Мягкие паруса, форма которых сохраняется только при плавном обтекании воздушным потоком обеих сторон, работают иначе, чем жесткое крыло. Кривизна паруса определяется отношением &delta / C (рис. 4.1).
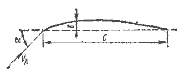
Рис. 4.1. Профиль паруса.
Совершенно плоский парус работает неэффективно, так как у передней шкаторины происходит срыв потока. С увеличением кривизны величина аэродинамической подъемной силы возрастает, но еще быстрее растет лобовое сопротивление. Для каждой скорости ветра VA и угла атаки а существует оптимальная величина кривизны паруса. В слабый потер при а = 30° будет оптимальной 10—15%-ная кривизна. Для быстроходных парусных судов, о которых идет речь, характерно движение под острым углом к ветру. В этих обстоятельствах наиболее эффективно работают паруса с кривизной профиля 3—5%, установленные иод углом атаки, равным 10—13°. Максимальная кривизна не должна располагаться слишком близко от передней шкаторины, так как при этом происходит срыв потока и увеличивается лобовое сопротивление. Для парусов с передней шкаториной, не закрепленной на мачте, это расстояние примерно равно 35% длины хорды, а для грота— не менее 10%.
Суммарную площадь парусности современной яхты образуют нс один, а несколько парусов, поднимаемых на одной или нескольких мачтах. При определении минимального числа мачт руководствуются следующими соображениями:
1) 30-50 м2 в одном парусе представляет предел, с которым может управиться один человек;
2) возможность использования «щелевого эффекта», заключающегося в том, что воздушный поток, получивший ускорение при обтекании впереди расположенного паруса, более эффективно взаимодействует с парусом, расположенным следом;
3) возможность взятия рифов (уменьшения площади паруса) при минимальном смещении центра парусности.
Первое условие действует, пока ручные лебедки не заменяются приводными. Такое оборудование, вполне доступное для крупных морских парусников, вовсе не подходят для высокоскоростных многокорпусных судов, остро реагирующих на дополнительный вес.
С увеличением количества парусов подъемная сила возрастает, но еще в большей мере увеличивается сила сопротивления. Для уменьшения угла аэродинамического сопротивления, т. е. повышения скорости движения по генеральному курсу, целесообразнее использовать один парус. Этот факт с учетом практически возможных размеров паруса и требований центровки при взятии рифов приводит к выводу, что более оправдана расстановка мачт не вдоль, а поперек судна. Вариант подобного вооружения установлен на катамаране Клифтон Флейшер (рис. 4 2).

Рис. 4.2. Катамаран Клифтон Флейшер.
Прежде чем обсуждать достоинства этого типа вооружения, остановимся на вопросе разумности применения жестких или и полужестких парусов.
В общем случае, по сравнению с одиночным мягким парусом, жесткий имеет более высокое аэродинамическое качество (отношение L / D) и аэродинамическую силу FA, в связи с чем ему отдают предпочтение при вооружении гоночных катамаранов класса С. Платой за эти преимущества являются больший вес и более высокий момент инерции при килевой и бортовой качке. Наглядной иллюстрацией этих соотношений жесткого и мягкого парусов явились результаты гонок 1976 г. на приз Малый кубок Америки, в которых американскому катамарану Аквариус с мягким парусом противостоял австралийский Мисс Найлекс с жестким парусом-крылом. В свежий ветер избыточный нес (82 кг) оказался более важным фактором, чем высокое аэродинамическое качество жесткого паруса; австралийский катамаран не смог опередить американцев ни в одной гонке. Для яхт открытого моря парусное вооружение, площадь которого ие может быть уменьшена взятием рифов, вообще не представляется приемлемым.
Итак, вариантом оптимального может быть парусное воорженне, показанное на рис. 4.3.
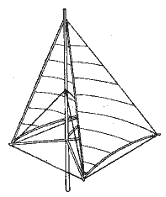
Рис. 4.3. Пирамидальное парусное вооружение.
Два треугольных паруса, соединенных вершинами, имеют между собой зазор, равный хорде паруса по всей высоте. У парусов достаточно большое удлинение и, в то же время, их общий центр давления располагается не так высоко, как у классических косых парусов той же площади. Экспериментально установлено, что центр давления, расположенный на 1/3 высоты треугольного паруса, при изменении угла атаки от минимальной величины до 90° перемещается ка расстояние 36—60% хорды от передней шкаторины. Расположив 35% площади паруса перед мачтой, можно получить вооружение, у которого центр давления всегда будет близ оси поворота (мачты), поэтому даже в свежий ветер шкоты не придется выбирать лебедкой.
Положительным качеством пирамидальных парусов является возможность обтянуть стоячий такелаж до установки вооружения на судно. Корпус и поперечные связи оказываются избавленными от нагрузок, которые они испытывают при обычном вооружении. Пирамидальное вооружение крепится на опорном подшипнике, как показано на рис. 4.4. Ниже четырех горизонтальных гиков установлен опорный роликовый подшипник с роликами из тефлона (рис. 4.4,6). Еще один подшипник устанавливается на топе мачты, если предусматриваются штаги, идущие к носовым и кормовым оконечностям корпусов, однако, если удлинение парусов не слишком большое, проводка штагов не обязательна.
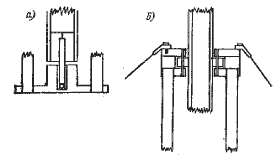
Рис. 4.4. Опорный и обжимной подшипники вращающейся мачты.
Многие конструкторы отдают предпочтение парусу-крылу, парусу с большим чистом сквозных лат и другим приспособлениям, позволяющим за счет более высокого аэродинамического качества уменьшить требуемую площадь парусности. В общем, речь идет о необходимости, обеспечивая максимальную силу тяги, иметь приемлемый крепящий момент, минимальный вес и предельную простоту управления. Эти требования наилучшим образом удовлетворяются при установке пирамидального вооружения.
Для оценки силы тяги паруса при заданной силе ветра необходимо, прежде всего, определить статическую остойчивость судна. На рнс. 4.5,а изображен катамаран в положении на ровный киль при нулевых значениях приложенной х парусу силы дрейфа Fy, и гидродинамической силы LH. Когда Fy = LH > 0, судно получает крен на угол θ в результате плавучесть наветренного корпуса уменьшается до пулевой при θ = 10— 12°.
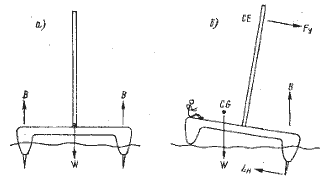
Рис. 4.5. Статическая остойчивость катамарана: а — при положения на ровный киль; б — при наличии крена.
Силы, действующие на катамаран при максимальном восстанавливающем моменте, показаны ка рис. 4.5, б. Восстанавливающий момент без учета сил, действующих на киль и парус, можно представить выражением (формула (4.7) имеет весьма приближенный характер, гак как предполагает линейную зависимость изменения объема корпусов от угла крена. — Прим, научн. ред.)
Nкорп = W (ȳ cosθ – ž sinθ) - b B0 (1 – θ/θ0)
| (4.7) |
где W —общий вес судна; y—расстояние по горизонтали от оси крека на подветеренном корпусе до центра тяжести — CG (половина расстояния b между диаметральными плоскостями корпусов), z — высота СG, В0 — водоизмещение наветренного корпуса в положении судна на ровный киль (без учета веса команды В0 = W/2). θc — угол крена, при котором наветренный корпус полностью выходит на воды. С увеличением угла крена θ уменьшаются (рис. 4.6) силы тяги Fx, и дрейфа Fy в первом приближении пропорционально cos2θ.
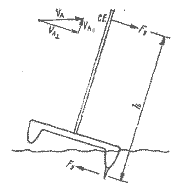
Рис. 4.6. Остойчивость катамарана на больших углах крена.
Кренящий момент от действия пары сил, приложенных к килю и парусу, составляет
Nпарус/киль = h Fy = h Fy1 cos2θ
| (4.8) |
h Fy1 = 1/2 · pa Va2ASCy
| (4.9) |
В качестве примера рассмотрим судно, имеющее следующие характеристики: W = 1130 кг; ȳ = 3 м; ž = 0,6 м; b = 6 м; B0 = 565 кг, θ = 12°. Уравнение восстанавливающего момента запишется
Nкорп = 3300 cos θ – 660 sin θ – 6780 (1 – θ/12)
| (4.10) |
где последний член равен нулю при θ > 12°. Парусное классическое вооружение (шлюп, кэч, шхуна и т. л.) примем площадью 46,5 м2 с относительным удлинением, равным 3, расстояние между центром давления ветра и центром бокового сопротивления корпуса h = 6,1 м, в том числе 2,1 м от нижней шкаторины паруса до центра бокового сопротивления и 3,9 м как треть высоты паруса. Тогда кренящий момент вегра составит
Nпарус/киль = 0,767 Va2 cos2θ, кГм
| (4.11) |
где Va выражена в узлах, а коэффициент Cy = 1. (1 ф·фт = 0,0227 кГм, прим. ГШ)
Чистый восстанавливающим момент в зависимости от θ и Va будет равен разности уравнений (4.10) и (4.11). Графическое решение приведено на рис. 4.7.
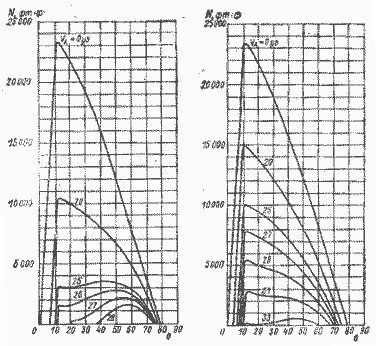 | ||
| Рис. 4.7. Кривые восстанавливающего момента катамарана с классическим парусным вооружением. | Рис. 4.8. Кривые восстанавливающего момента того же катамарана с пирамидальным парусным вооружением. | |
Как видно из диаграммы, с повышением силы ветра кривая остойчивости имеет тенденцию к выравниванию. Этим объясняется тот факт, что катамараны могут ходить с креном 40—50°, а при 50—60° — достигать второго пика остойчивости (см. рис. 4.7, 4.8). Если принимать наибольшую величину ходового крена равной той, при которой наветренный корпус отрывается от воды, то для рассмотренного примера он обеспечивается при вымпельном ветре не более 26 уз.
Сравним остойчивость такого же катамарана с пирамидальным вооружением. Относительное удлинение парусов примем равным 3. как и в предыдущем примере. Угол наклона парусов составит около 19,5°. Чтобы компенсировать потерю тяги, вызнанную наклонным положением парусов, увеличим их площадь до AS = 46,5/cos2( 19,5°) = 52,3 м2. В этом случае h = 4,9 м (при том же расстоянии от СE до нижней шкаторины паруса). Кренящий момент пирамидального вооружения с углом наклона парусов Ф и площадью парусности AS составит
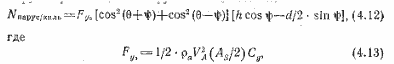
a cl — расстояние между центрами давления парусов, равное 2/3 расстояния у нижних шкаторин. Для рассматриваемого примера уравнение (4.12) будет иметь вид
Nпарус/киль = 0,28 Va2 [cos2(θ + 19,5) + cos2(θ – 19,5)]
| (4.14) |
Как и в предыдущем случае, чистый восстанавливающий момент в зависимости от θ и Va получим в виде разности уравнений (4.10) и (4.14).
Результат представлен на диаграмме рис. 4.8. Сравнивая его с рис. 4.7, видим, что катамаран с пирамидальным парусным вооружением при той же силе ветра имеет меньший крен и способен сохранить положительную остойчивость при большей силе ветра, чем судно с обычными парусами, а следовательно, создается большая сила тяги. Ходовой хрен θ = 12° на катамаране с пирамидальным вооружением выдерживается при скорости вымпельного ветpa до 32 уз, в то время как для судна с обычными парусами эта величина составляет 26 уз, что обеспечивает около 43% дополнительной тяги.
Сопоставляя диаграммы, находим, что катамаран с пирамидальным вооружением не обеспечивает ту безопасность, которая имеет место при обычном вооружении, так как на диаграмме остойчивости (рис. 4.8) отсутствует второй пик. Этот недостаток до некоторой степени компенсируется возможностью быстрого реагирования на порывы ветра благодаря чрезвычайной простоте управления пирамидальными парусами.
Для обычного вооружения проблемой является скручивание паруса. Системы оттяжки гика в сочетании с проложенным по всей ширине судна погоном гика-шкота позволяют до известной степени выправить форму паруса, неконтролируемое же скручивание является причиной потери 10—15% силы тяги. У пирамидального вооружения все три угла паруса жестко раскреплены и скручивание практически исключено.
В попутный ветер при обычном вооружении трудно обеспечить эффективную работу всех парусов. Для пирамидального вооружении, разворачивающегося на 360°, оптимальный угол атаки выбирается по скорости, показываемой лагом. В любом случае обеспечивается эффективная работа обоих парусов (рис. 4.9).
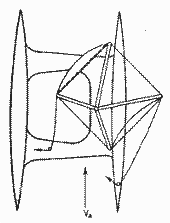
Рис. 4.9. Работа пирамидального парусного вооружения при попутном ветре.
Для проа важно иметь паруса, которые бы позволяли менять направление движения (идти кормой вперед). Решение именно этой проблемы и навело меня на идею пирамидального вооружения, которое легко заставить работать в противоположном направлении. Это качество дополнительно представляет интерес для движения задним ходом при маневрировании под парусами, что на обычном вооружении невозможно.
Итак, по пропульсивным качествам (сопротивлению) преимущество имеют суда больших размерений. Это же справедливо и в отношении поперечной остойчивости. Восстанавливающий момент представляет собой произведение веса (величины порядка L3) на плечо и, следовательно, является величиной порядка L4, тогда как аэродинамический кренящий момент, пропорциональный произведению площади парусности АS на высоту центра давления h — на порядок меньшая величина (L3). Отсюда судно больших размерений может нести паруса большей площади на единицу водоизмещения, что потенциально обеспечивает преимущество в скорости, пропорциональное L½. В заключение можно сказать, что наиболее эффективным вооружением быстроходных многокорпусных судов будут легкие (без лат) пирамидальные паруса с удлинением А ≈ 3. Величина дополнительного сопротивления, вызываемая четырьмя гиками, с избытком компенсируется за счет увеличения эффективно работающей площади парусов.
Встречный поток обтекает подводную часть корпуса и киль под углом дрейфа λ, вызывая гидродинамическую силу FH, равную и противоположную по направлению аэродинамической сале FA. В этой главе будут рассмотрены условия образования гидродинамической силы, обеспечивающей минимальное значение угла гидродинамического сопротивления δH.
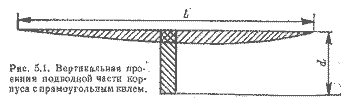
На рис. 5.1 изображена вертикальная проекция подводной части корпуса с прямоугольный килем. Определяя гидродинамическую подъемную силу и сопротивление, рассмотрим киль и корпус отдельно. По Кастлу, запишем выражение для коэффициента подъемной силы
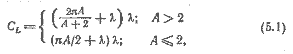
где λ выражен в радианах, а относительное удлинение определяется выражением
A = 2 D2 / AK
| (5.2) |
для киля, где AK — его площадь до ватерлинии (gри больших углах дрейфа из (5.1) следует одинаковый характер нелинейности зависимости СL от λ для крыльев большого и малого удлинения. В действительности эта нелинейность становится существенной лишь для крыльев малых удлинений. — Прим. научн. ред.).
Для корпуса в аналогичном выражении вместо AK записывается AP – вертикальная проекция подводной части корпуса, а половина размаха принимается равной осадке Н. Для полукруглого сечения H = В/2, AP = AF / π, где AF – площадь смоченной поверхности (2.20). Относительное удлинение такого корпуса равно
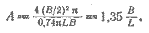
| (5.3) |
Для нас представляет интерес А в пределах от 0,04 до 0,12. Индуктивное сопротивление характеризуется коэффициентом
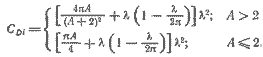
| (5.4) |
Общее гидродинамическое сопротивление будет найдено как сумма лобового сопротивления, определенного по формуле Хавелока — Кастла (см. гл. 2), и индуктивного сопротивления корпуса и киля
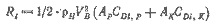
| (5.5) |
для угла дрейфа λ. Из рассмотренного полного гидродинамического сопротивления и полной подъемной силы, определенной по формуле
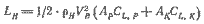
| (5.6) |
для различных углов дрейфа, можно установить, что максимальное значение отношения подъемной силы к сопротивлению (гидродинамическое качество) или минимальный угол гидродинамического сопротивления δH достигается при λ = 4—5°. (Угол дрейфа, при котором достигается минимальное значение угла гидродинамического сопротивления, зависит от удлинения системы элементов, создающих сопротивление дрейфу, и может отличаться от указанного автором. — Прим. научн. ред.)
Остановимся на выборе размеров киля. Решение может быть получено приравниванием подъемной гидродинамической силы и боковой составляющей аэродинамической силы, приложенной к парусу
Fg = 1/2 &ro;aVA2 ASCy
| (5.7) |
где
Cy = CLcosβ + CDsinβ
| (5.8) |
Таким образом, необходимо знать курсовой угол β (VT, γ) и, следовательно, отношение VB / VT для того, чтобы определить площадь киля, н наоборот. Если находят только максимальную площадь киля для корпуса с малой величиной отношения водоизмещения к длине, подъемной силой самого корпуса можио пренебречь, как это показано на рис. 5.2 для тримарана Галлиард, спроектированного Ньюиком.
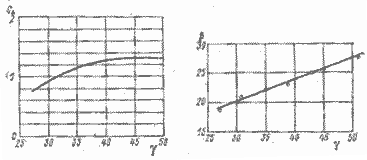 | ||
| Рис. 5.2. Зависимость коэффициента аэродинамической силы от курсового угла к истинному ветру тримарана Галлиард. | Рис. 5.3. Зависимость величины β от γ тримарана Галлиард. | |
Для острых к ветру курсовых углов CA ≈ Cy, поэтому Cy ≈ 1 для курса бейдевинд в широком диапазоне углов β.
Приравняв уравнения (5.6) при CL, P =0 и (5.7) при Cy =1, найдем
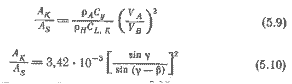
где коэффициент CL, P принят равным 0,35, что соответствует относительному удлинению А = 6 и углу дрейфа &lambda = 4°. Выражение в квадратных скобках получено из треугольника скоростей (см. рис. 1.1) согласно теореме синусов, величина β для различных γ применительно к тримарану Галлиард дана на рис. 5.3. С помощью этого графика на рис. 5.4 построена кривая зависимости (5.10).
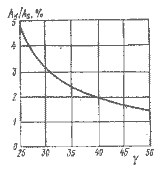
Рис. 5.4. Оптимальные соотношения площадей киля и парусов для различных курсовых углов γ.
Исходя из нее, максимальную площадь киля можно установить равной AS. Конечно, в идеальном случае желательно иметь возможность изменять площадь киля.
Здесь мы подходим к выбору между швертом (откидным и кинжальным) и шверцами.
Достоинством откидного шверта является безопасность эксплуатации: при ударе о подводное препятствие он свободно уходит в колодец. Длинная щель в днище, необходимая для шверта большего удлинения, дает, однако, дополнительное сопротивление. Кроме того, воспринимаемые швертом усилия создают значительные напряжения в конструкциях швертового колодца, его приходится делать повышенной прочности, что увеличивает вес.
Устройство с кинжальным швертом не нуждается в длинной щели, так как он перемещается вертикально. Его недостатком является отсутствие надежной защиты от ударов о мель. Д. Ньюик, предпочитающий именно этот тип швертового устройства, применяет специальные, заполненные в кормовой части пенопластом, колодцы, которые, до известной степени, предотвращают крупные поломки. Швертовые устройства обоих типов, устанавливаемые, как правило, в корпусе, создают проблемы с их размещением. Шверцы имеют в этом отношении преимущество перед швертами, с успехом служа при плавания на мелководье. Возможность перемещения оси поворота вдоль борта позволяет легко регулировать центровку, совмещать на одной вертикали центр давления на парусе и центр бокового сопротивления. Шверцы применимы даже з случае, когда глубина достаточна только для корпуса судна. Для их установки не нужен колодец, они легко доступны для ремонта, не подвержены повреждениям, которые вызывают грунт и мелкие камни, попадающие в швертовый колодец.
Недостатков у шверцевого устройства сравнительно немного. Это необходимость поднимать один и опускать другой шверц при смене галсов, что на тримаране или катамаране с самоустанавливающимся пирамидальным парусным вооружением не вызывает сложности. В связи с тем, что шверц представляет собой крыло, пересекающее поверхность воды, имеется опасность вентиляции —— подсоса воздуха на стороне пониженного давления (см. более подробно в гл. 6). Этот недостаток устраним: достаточно поставить ннже ватерлинии шайбу или придать шверцам небольшой наклон вперед, как рекомендует Д. Кейпер. Просто удивительно, почему шверцы до сих пор не нашли применения на гоночных многокорпусных судах; наверное, единственной тому причиной является то, что конструкторы не представляют их иначе, как в сочетании с тихоходными баркасами, по сей день плавающими по р. Темзе.
Еще одна интересная возможность заключена в конструкции шверцевого устройства: можно не только перемещать его вдоль борта, но и предусмотреть установку под различными углами атаки за счет поворота вокруг вертикальной оси. Таким образом удается уменьшить или даже исключить дрейф судна, а следовательно, и индуктивное сопротивление корпуса. За счет применения ассиметричного профиля снижается индуктивное сопротивление и самих шверцев при сохранении величины подъемной силы.
Теперь рассмотрим руль. Назначение руля — создавать отклоняющий момент с целью изменения курса. На высокоскоростных парусных судах находят применение навесные (за транцем) рули, рули, подвешенные к скегу, полубалансирные рули (рис. 5.5).

Рис. 5.5. Три типа рулей, применяемых на быстроходных парусных судах.
Гидродинамическое качество руля (отношение L / D) не имеет такого значения, как для крыльев. Его эффективность в гораздо большей мере определяется достижимой максимальной величиной боковой силы при отклонениях руля и минимальной величиной сопротивления при установке пера руля в диаметральной плоскости.
Необходимая площадь руля зависит от его формы и относительного удлинения, однако средняя величина может быть принята равной
AR ≈ 0,07 (AP + AK
| (5.11) |
Проектируя руль, принимают компромиссные решения. Для того чтобы обеспечить плавное обтекание, исключить прорыв воздуха с поверхности, перо руля должно быть опущено достаточно глубоко, но не настолько, чтобы способствовать увеличению крена. Так же непросто выбрать и величину относительного удлинения. При большом удлинении, как уже говорилось, для заданного угла атаки гидродинамические силы на единицу площади выше, чем при малом. В этом случае срыв потока возникает на меньшем угле атаки. Существует значение относительного удлинения, которое дает наибольшую величину боковой силы на единицу площади: для полубалансирного руля она равна примерно единице, для руля за скегом — 0,5—1 (с учетом площади самого скега}; для навесного (за транцем} руля 1—2.
Выбирая форму поперечного сечения, нужно учитывать, что острая передняя кромка способствует срыву потока на малых углах атаки. Предпочтительнее придавать передней кромке эллиптическую форму, а сечение всего руля выполнять в виде профиля с максимальной толщиной, равной 12% хорды, расположенной на 1/3 длины хорды от передней кромки. В большинстве случаев применяют небалансирные рули, центр давления которых смещен от оси вращения на любом угле атаки. Экспериментально установлено, что центр давления располагается на расстоянии 20—25% длины хорды от передней кромки на малых углах атаки и примерно на 40% при перекладке из большой угол. Следовательно, ось поворота руля должна помещаться в пределах 20% ширины пера от передней кромки. На многокорпусных судах во избежание поломки небаланс центра давления и осн поворота принимается минимальным.
На катамаранах принято устанавливать по рулю на каждом корпусе. В этом случае уравнение (5.11) используется для расчетов каждого руля отдельно. На тримаранах, как правило, руль ставится только на главном корпусе. Руль быстроходных судов должен быть достаточно прочным. Наилучшим образом этот вопрос решается при установке руля за скегом, так как в этом случае он раскреплен у верхней и нижней кромок, тогда как рули двух других типов крепятся как кронштейны (см. рис. 5.5). Пример компромиссного решения показан на рис. 5.6. Перо руля вместе с предкрылком-скегом опущено через колодец типа швертового, расположенный вплотную к транцу.
Особый подход требуется к выбору рулевого устройства для проа. В связи с тем, что эти суда рассчитаны на реверсивное плавание, рули устанавливаются в обенх оконечностях, при этом они должны иметь устройство для подъема или для синхронизации совместной работы. На проа Чирс в 1968 г. два руля в комбинации со швертами были установлены в обеих оконечностях наветренного корпуса. Перо руля размешалось в средней по высоте части шверта и работало только когда шверт опускался до конца, Это позволяло использовать частично опущенный передний шверт для повышения устойчивости судна на курсе. Устройство схематично показано иа рис. 5.7.
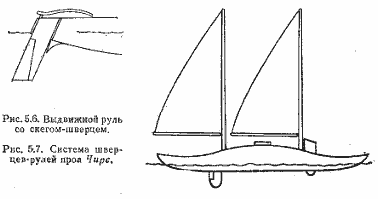
На проа 1974 г. Ньюик установил неподъемные полубалансирные рули, на каждой оконечности подветренного корпуса. Эти рули действовали совместно, толкая корму в одну сторону, а нос в другую. Эта система проще установленной на Чирсе, где при каждом повороте требовались сложные манипуляция, включающие перенос румпеля с одной оконечности на другую, однако и то и другое не обеспечивает безопасности в случае посадки на мелью.
Итак, рассмотрены системы, обеспечивающие сопротивление дрейфу и управляемость судна. Прежде чем переходить к конкретным конструкциям, остановимся на проблеме устойчивости судна на курсе. Для однокорпусных яхт устойчивость движения зависит от крена. Когда на остром курсе яхта уваливается под ветер, сила дрейфа и величина крена возрастают. Линия действия аэродинамической силы FA при этом смещается под ветер от линии действия гидродинамической силы FH, возникающий в результате момент приводит судно к ветру. Уменьшение крена в свою очередь ограничивает приведение к ветру, и в итоге судно имеет тенденцию удерживаться на заданном курсе. На попутных курсах изменение крена дает противоположный результат. Когда, например, на курсе галфвинд яхта уваливается, крен уменьшается, и уход с курса еще более увеличивается. Можно сделать общее заключение, что яхты обычно (не все и не всегда) хорошо удерживаются на острых курсах, но обнаруживают рыскливость при попутных.
У многокорпусных судов способность к удержанию на курсе проявляется более сложно. Рассмотрим эффект, связанный только с парусами. На рис. 5.8 показан катамаран с одномачтовым малого удлинения вооружением, внезапно уклонившийся от курса по часовой стрелке.
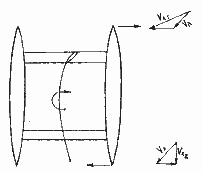
Рис. 5.8. Аэродинамика катамарана при внезапном уклонении от курса (рыскании).
Возникающая при этом боковая составляющая скорости, суммируясь со скоростью ветра VA, создает вымпельный ветер FA2 иFA2. Угол атаки у передней шкаторины возрастает, у задней уменьшается. Смещение распределения давления ветра к передней шкаторине создает корректирующий вращающий момент, который разворачивает судно против часовой стрелки. Этот эффект сильнее проявляется при малых значениях относительного удлинения паруса или двухмачтовом вооружении.
Если судно медленно приводится к ветру, угол атаки паруса в целом уменьшается. Описанный эффект уже не будет иметь места. Однако, как известно, при уменьшении угла атаки центр давления ветра из парус смещается вперед, что также создает корректирующий вращающий момент, превосходящий действие сил, уклоняющих судно с курса. И этот эффект проявляется сильнее при парусах малого относительного удлинения. Ма двухмачтовом судне устойчивость па курсе можно повысить, если бизань будет выбрана слабее, чем передние паруса. В случае непроизвольного уваливания сила тяги бизани возрастает больше, чем у передних парусов, за счет этого корма заносятся под ветер, и судно возвращается на курс. Напротив, на приводке бизань первой обезветрится, и судно будет уваливаться.
Работа киля при удержании судна на курсе протекает так же, как и у парусов. Отсюда понятно, почему строившиеся 50 лет назад яхты с длинными фальшкилями великолепно держали курс, в то время как, например, современные яхты 12-метрового класса доставляют команде немало хлопот. Киль малого удлинения не находит сейчас применения из-за большой смоченной поверхности. Лучший результат дает установка на достаточном расстоянии друг от друга двух килей большого удлинения (рис. 5.9).
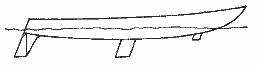
Рис. 5.9. Система килей, обеспечивающая устойчивость на курсе.
Главный киль располагается в районе вращения (у центра бокового сопротивления), а вторым может служить навесной руль, как это имеет место на швертботах. Эта система позволяет удерживать судно на курсе при установке подруливающих устройств (флюгерного или связывающего шкоты с румпелем), и все же без ручного управления она недостаточно надежна. Лучший результат может быль получен благодаря подвеске руля на скеге значительной площади. Влияние киля на устойчивость движения по курсу усиливается эффектом, создаваемым благодаря изменению угла атаки. При уваливании под ветер на острых курсах скорость хода возрастает. Боковая сила изменяется сравнительно медленно, поэтому возрастание скорости сопровождается уменьшением угла дрейфа λ. Центр бокового сопротивления с уменьшением угла дрейфа перемещается вперед, Это создает момент, корректирующий положение судна на курсе.
На попутных курсах уваливание под ветер сопровождается дестабилизирующим эффектом, так как скорость хода уменьшается. На практике, при наличии двух килей большого относительного удлинения как стабилизирующий, так и дестабилизирующий эффект, создаваемый изменением угла дрейфа, пренебрежимо мал. Эффект, создаваемый слабо выбранной бизанью, может быть усилен слегка переложенным на ветер рулем. Потеря либо увеличение подъемной силы на руле происходит быстрее, чем на киле, что создает необходимый корректирующий момент. Имеется убедительный аргумент в пользу установки шверцев не по бортам главного корпуса тримарана, а по бортам его аутригеров.
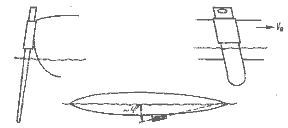
Рис. 5.10. Установка шверца.
Если шверцы развернуты (рис. 5.10), то в случае приведения к ветру подъемная сила подветренного шверца увеличивается на столько же, на сколько она уменьшается у наветренного, что создает вращающий момент. В целом физическая картина аналогична наблюдаемой у катамаранов с асимметричными корпусами (см. гл. 2).
Таким образом, катамараны и тримараны целесообразно оснащать рулями, подвешенными к скегам, как это показано на рис. 5.6, и шверцами в коробах, допускающих их аварийное откидывание. Глубина погружения шверцев устанавливается их подъемом. Вариант такого устройства представлен на рис. 5.10.
Лучшая система, обеспечивающая управляемость при достаточно высоком сопротивлении дрейфу и стабилизации на курсе, для проа состоит из двух регулируемых шверцев-рулей, установленных на оконечностях подветренного аутригера. Принципиально устройство не отличается от показанного на рис. 5.10, за исключением того, что шверцы устанавливаются с нулевым углом атаки и нижняя их часть дополняется рулями. Синхронное управление обоими рулями осуществляется штурвалом, расположенным в средней части судна. Самыми сложными являются операции по развороту шверцев на 180° и установке нх в сбалансированной позиции, при которой носовой шверц поднят выше кормового. Это выполняется талями или (на больших проа) гидроприводом (рис. 5.11).
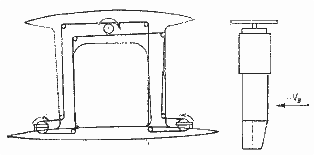
Рис. 5.11. Система управления рулями на проа.
Тенденция рассматривать подводные крылья только как средство для подъема корпуса судна над водой идет от их применения па судах с механическими двигателями, которые находятся под воздействием гораздо меньшего набора сил, чем парусники. Количественная зависимость сопротивления (отношение веса судна к сопротивлению) от отношения VB / L½ приведена на рис. 6.1 для типичного многокорпусного судна и для того же судиа, снабженного подводными полностью погруженными крыльями.
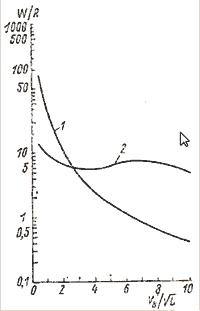
Рис. 6.1. Подъемная сила и сопротивление.
1 – для узких корпусов, 2 – для подводных крыльев.
Из графика видно, что вплоть до относительной скорости VB / L½ = 9,5 отношение веса к сопротивлению у водоизмещающего. корпуса больше, чем у корпуса с подводными крыльями. Достижение таких высоких скоростей возможно при условии, что судно выдерживает значительный кренящий момент и несет при этом паруса, расположенные близко к вертикальной плоскости. Для обеспечения этих качеств и была выдвинута идея применить подводные крылья на парусных судах. Впервые их применили для стабилизации движения парусников с аутригерами на Мадагаскаре и в Дар-эс-Саламе. Э. Брюс первый правильно объяснил физические принципы их работы. Судно с наклонным подводным крылом на подветренном аутригере изображено на рис. 6.2.
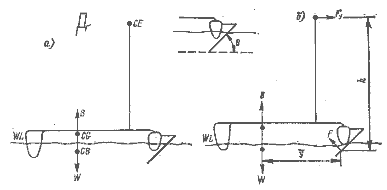
Рис. 6.2. Статическая и динамическая остойчивость проа с подводными крыльями Брюса.
Действие только статических сил — веса W и противостоящей ему и направленной по той же вертикали силы плавучести В представлено на рис. 6.2, а. Рис. 6.2, б показывает судно в состоянии динамического равновесия, двигающееся с некоторой постоянной скоростью. В этом случае сила поддержания будет находиться на одной вертикали с силой веса при отсутствии кренящего момента. Если это условие нарушится, центр сил поддержания сместится под ветер, и судно получит крен. Тело сохраняет состояние равновесия, если оно не испытывает действия несбалансированных сил в горизонтальном либо вертикальном направлениях. Необходимо также, чтобы моменты сил относительно любой точки равнялись нулю. Исходя из вышеизложенного, пренебрежем движущей силой и силой сопротивления, из условия равновесия сил получим
B = W – F cos θ
| (6.1) |
и
Fy = F sin θ
| (6.2) |
Помножив обе части выражений (6.1) yf sin θ и (6.2) на cos θ (θ — угол наклона крыла) и сложив их, получим
В sin θ + Fy cos θ = W sin θ или Fy = (W – B) tg θ
| (6.3) |
На основании (6.1) устанавливаем, что вертикальная составляющая силы, действующей на крыло, равна
F cos θ = Fy сtg θ
| (6.4) |
С учетом (6.4) уравнение для силы поддержания выразится
B = W – Fy сtg θ
| (6.5) |
Таким образом, исследование динамического равновесия парусного судна на подводных крыльях может быть сведено к рассмотрению диаграммы сил, представленной на рис. 6.3.
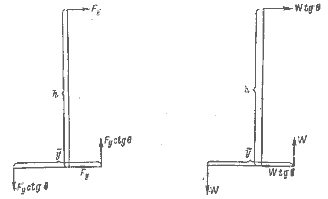 | ||
| Рис. 6.3. Диаграмма сил, действующих до выхода проа на крыльевой режим. | Рис. 6.4. Диаграмма сил, действующих после выхода проа на крылья. | |
Прнвяв за нуль равенство моментов относительно некоторой точки, придем к следующему основному выражению:
Fy (h – y сtg θ) = 0
| (6.6) |
Поскольку, кроме тривиального статического случая, Fy никогда не равно нулю, величина в скобках должна обратиться в нуль, чтобы обеспечить компенсацию кренящего момента. Тогда
у – h сtg θ
| (6.7) |
Определив соотношение параметров, при котором кренящий момент равен нулю, зададимся следующими вопросами. Как велика может быть сила Fy, (или, что то же самое, какая парусность допустима для заданной силы ветра), чтобы удовлетворять уравнению (6.6)? Ответ на этот вопрос дает зависимость (6.5). Это уравнение показывает, что сила поддержания уменьшается при увеличении Fy или вертикальной составляющей силы давления на крыло. С приближением значения Fy к величине W tg θ сила поддержания стремится к нулю. При этом корпус выходит из воды. В момент отрыва корпуса диаграмма сил приобретает вид, показанный на рис. 6.4. Составляющая сила давления ветра Fy ctg θ, которая создает восстанавливающий момент, достигает максимальной величины, равной W; соответственно восстанавливающий момент будет равен
Nmax = W у
| (6.7) |
Увеличение Fy, сверх значения W tg θ приведет к опрокидыванию. Та же величина максимального восстанавливающего момента будет получена, если заменить крыло легким непотопляемым поплавком. Достоинства устройства с наклонным крылом на подветренном корпусе, известного как подводные крылья Брюса, заключаются в компенсации крена лри всех обстоятельствах, вплоть до полного отрыва корпуса от воды, благодаря чему паруса работают с максимальным эффектом; а также з том, что сила FH, создающая крен, превращается в подъемную силу, уменьшающую сопротивление корпусов.
Кренящий момент может быть компенсирован и путем установки на наветренном корпусе наклонного подводного крыла, которое в большей мере прижимает, чем поднимает корпус – (рис. 6.5).
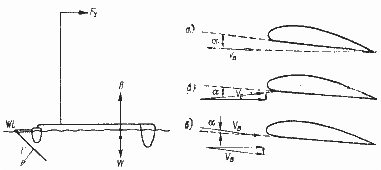 | ||
| Рис. 6.5. Подводное крыло системы Брюса, установленное на наветренном аутригере. | Рис. 6.6. Изменение угла атаки при вертикальном перемещении крыла. | |
Этому типу крыльевого устройства присущи, однако, два больших недостатка. Во-первых, когда корпус прижимается к воде, его сопротивление с ростом силы Fy; быстро увеличивается. Во-вторых, и это особенно важно, установка крыльев иа наветренной стороне не обеспечивает устойчивого режима работы. Если подветренное крыло под действием волн оторвется от воды, кренящий момент мгновенно погрузит его образно. Напротив, в аналогичной ситуации наветренное крыло, потеряв связь с водой, уже не обеспечит откренивания и опрокидывание будет неотвратимо. По этим причинам подветренные крылья Брюса или крылья, имеющие угол наклона θ такой, что удовлетворяется условие y = h tg θ, обеспечивают наилучшую вертикальную к боковую стабилизацию.
Выбирая угол наклона крыла, следует считать наиболее приемлемой величину θ = 40 – 45°. Большие величины θ для удовлетворения зависимости (6.7) потребуют слишком большого увеличения ширины судна. Если θ очень мал, необходимо увеличить площадь крыла либо мириться с большим углом дрейфа, создающего боковую силу, равную Fy.
Рассмотрим типы подводных крыльев, которые могут быть установлены на парусных судах. По принципу работы они делятся па полностью погруженные и пересекающие поверхность воды. Чтобы обеспечить вертикальную стабилизацию движущегося судна, необходимо устройство, которое бы «следило» за поверхностью воды н немедленно реагировало на перемещения относительно нее, возвращая судно в нормальное положение. Для этой цели на советских речных и морских судах используются полностью погруженные крылья, находящиеся под самой поверхностью воды, где подъемная сила зависит от глубины погружения. Специальное следящее устройство, которое реагирует на изменение глубины погружения, меняя угол атаки крыльев, было применено в проектах, осуществленных Хуком и другими конструкторами.
Рассмотрим схемы с крыльями пересекающими поверхность воды. В первом приближении подъемная сила подводного крыла при заданной скорости находится в линейной зависимости от глубины погружения и угла атаки α, под которым оно установлено относительно встречного потока воды. Как показано на рис. 6.6, а, перемещение крыла вниз (увеличение погружения) создает дополнительную скорость потока, вектор которой направлен вверх. В результате угол атаки возрастает (рис. 6.6, б). Перемещение крыла вверх, наоборот, уменьшает утоя атаки и подъемную силу; судно возвращается в первоначальное положение (рис. 6.6, в). Эффект совершенно аналогичный описанному в гл. 5, где рассматривалась устойчивость движения парусного судна на курсе. Таким образом, подводные крылья противодействуют любому вертикальному перемещению. Это свойство многократно возрастает у крыльев, пересекающих поверхность воды, благодаря автоматическому изменению их рабочей (погруженной) площади: непроизвольное заглубление увеличивает погруженную поверхность, за счет дополнительной подъемной силы судно всплывает, возникающее при всплытии уменьшение угла атаки смягчает это перемещение, делает его мало ощутимым.
Системы крыльев, пересекающих поверхность воды, могут состоять из одной или нескольких плоскостей (рис. 6.7). На спокойной воде монокрыло при плавании под парусом работает достаточно надежно, однако для открытого моря предпочтительнее многоступенчатые системы (лестничные подводные крылья). Наличие в такой крыльевой системе недогруженных крыльев обеспечивает необходимое приращение подъемной силы при встрече с волной. Монокрылья применяются, главным образом, на судах с механическим двигателем, эксплуатирующихся в достаточно узком диапазоне скоростей.
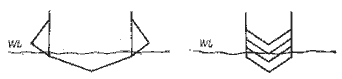
Рис. 6.7. Моно- и многоступенчатые крылья, пересекающие свободную поверхность воды.
На парусниках используемая мощность, а следовательно, и скорость, изменяются в широком диапазоне. В лестничных системах крылья могут иметь разный профиль. Сильно погруженные верхние крылья, установленные за уровне статической ватерлинии, обеспечивают большую подъемную силу при низком качестве (отношении L/D). Высокая скорость достигается при движении на нижних плоскостях. Исследуем работу крыльев на волнении. На рис. 6.8 показано перемещение частиц воды, когда волны движутся слева направо.
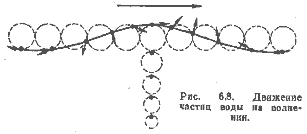
Рис. 6.8. Движение частиц воды на волнении.
Орбиты частиц у поверхности имеют диаметр, равный высоте волны. Рассмотрим движение парусника на подводных крыльях навстречу волне. Благодаря движению частиц воды на переднем склоне волны угол атаки и подъемная сила крыла увеличиваются, Судно всходит на волну. На обратном склоне угол атаки и подъемная сила крыла уменьшаются, судно огибает контур волны. Когда судно следует попутным курсом за волной н обгоняет ее, то на заднем склоне волны оно, из-за уменьшения угла атаки крыла, врезается в нее. Именно в этой ситуации в наиболее полной мере проявляются преимущества многоступенчатой крыльевой схемы.
Давление на выпуклой стороне крыла ниже, чем на плоской. Близ поверхности воды оно может быть меньше атмосферного. Если в образующуюся каверну проникнет воздух, произойдет потеря подъемной силы. Данное явление известно как вентиляция крыла. Ее предупреждают, устанавливая шайбу (рис. 6.9) или монтируя крылья и стойки под острым углом к направлению движения, за счет чего создается подъем воды, препятствующий вентиляции.
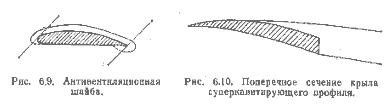 | ||
| Рис. 6.9. Антивентиляционная шайба. | Рис. 6.10. Поперечное сечение крыла суперкавитирующего профиля. | |
Этот способ был с успехом применен Кейпером на его крылатом тримаране Вилливо, совершившим рейс через Тихий океан.
Для заданных глубины погружения и геометрии крыла существует предел скорости, превышение которого ведет на отдельных участках поверхности крыла к возникновению кавитации, вызывающей эрозионные разрушения. Кавитация подводных крыльев возникает при скоростях более 40 уз и может рассматриваться применительно к парусникам только в случае рекордных скоростных судов. Для них могут найти применение многоступенчатые схемы с суперкавитирующими нижними крыльями (рис. 6.10).
Обратимся теперь к вопросу о размерениях и расположении крыльевых устройств при их использовании на парусных судах. Очевидно, крылья должны иметь большой размах. С учетом необходимости плавания в водоизмещающем режиме такие крыльевые устройства удобнее размещать на судах большой ширины, к которым в первую очередь относятся катамараны, тримараны и проа. Для катамаранов и тримаранов — судов, симметричных относительно диаметральной плоскости, крыльевые устройства также должны быть симметричны. Наиболее простые конструкция такого типа выполнены по самолетной схеме (рис. 6.11) или по схеме «утка» (ркс. 6.12).

Рис. 6.11. Катамаран Мейфлай конструкции Ф. Хамсфорда с самолетной схемой установки крыльев.

Рис. 6.12. Катамаран Флайинг Фиш конструкции Д. Нигга с расположением крыльев по схеме "утка".
Для самолетной схемы характерно переднее расположение основных несущих крыльев Брюса; управляемое кормовое крыло обеспечивает удифферентовку судна.
У крыльевого устройства, выполненного по схеме «утка», дифферентующее малопогруженное крыло установлено в носу, а крылья Брюса — ближе к корме. Вопрос о том, для какого типа судна следует предпочесть ту иле иную схему крыльевого устройства, зависит от его планировки и размещения экипажа, однако для тримарана, предназначенного для открытого моря, схема «утка» предпочтительнее. Заметим, что подводное крыло аналогично пружине с демпфированием благодаря изменению величины подъемной силы в зависимости от глубины и скорости изменения погружения.
Жесткость такой пружины пропорциональна степени изменения подъемной силы с глубиной погружения (малая хорда — жесткое крыло), а величина демпфирования — степени изменения подъемной силы в зависимости от угла атаки, который определяется скоростью вертикальных колебаний. При большой хорде крыло с малым углом атаки обеспечивает наиболее эффективное демпфирование колебаний. Если носовое и кормовое крылья имеют одинаковые характеристики или кормовое крыло более жесткое, возможна потеря вертикальной устойчивости движения, типа дельфинирования. На попутном волнении лучшая продольная устойчивость движения обеспечивается хорошо демпфирующим кормовым крылом и жестким носовым. Иными словами, необходимо, чтобы слабо погруженное носовое крыло работало с большим углом атаки, а кормовое, на которое ложится до 85% нагрузки, имело угол атаки, соответствующий максимальной величине отношения L/D. Аналогично у глиссирующего судна эти качества обеспечиваются широким плоским днищем в кормовой части и заостренной с большим развалом выше ватерлинии носовой оконечностью. Отсюда схема «утка» позволяет лучше контролировать килевую качку, чем самолетная. С точки зрения стабилизации бортовой качки обе схемы предоставляют примерно равные возможности. Если оба главных крыла имеют наклонные несущие плоскости (крыльевая система Брюса), то, в результате дрейфа, угол атаки подветренного крыла увеличивается, а наветренного уменьшается. Чтобы на любом курсе выполнялось условие, записанное в виде уравнения (6.7), ширина судна должна быть почти вдвое больше высоты до центра давления на парусе, что практически невозможно. Таким образом, судно с симметричных расположением крыльев испытывает крен, также уменьшающий подъемную силу наветренного крыла, которое частично или полностью обнажается.
Рассмотрим асимметричную крыльевую схему проа. Для обеспечения устойчивости по дифференту два крыла Брюса устанавливаются у носовой и кормовой оконечности легкого подветренного корпуса (рис. 6.13).

Рис. 6.13. Проа Тайгер конструкции Дж Чепмена с крыльями Брюса.
Носовое крыло должно вметь немного больший угол атаки, чем кормовое, для того чтобы обеспечить необходимый уровень демпфирования. Восстанавлизающий момент у проза с крыльями Брюса имеет большую величину, чем по уравнению (6.8), только при увеличении веса наветренного корпуса или установке на нем подводного крыла с отрицательным углом атаки, создающего силу, направленную вниз.
Стоувер предлагает с возрастанием скорости и кренящего момента увеличивать вес наветренного корпуса приемом в него водяного балласта. Недостатком такого решения является увеличение сопротивления н невозможность быстро восстановить нормальную плавучесть наветренного корпуса. Крыло с отрицательным углом атаки также влияет на рост сопротивления, так как крыльям Брюса при этом приходится не только принимать на себя вес судна, но и компенсировать силу К, действующую на наветренное крыло. Приняв для этого случая. отношение подъемной силы крыльев к их сопротивлению равным 10, можно показать, что эффективное отношение горизонтальной подъемной силы и сопротивления, служащее мерой угла гидродинамического сопротивления δH, равно
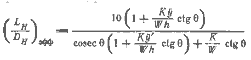
| (6.9) |
где К-- направления вниз сила наветренного крыла
К = Fy ctg ф – W
| (6.10) |
а y — расстояние от точки ее приложения до центра бокового сопротивления крыльев Брюса. Для больших значений K/W, уравнение (6.9) будет приближаться к пределу
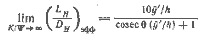
| (6.11) |
который соответствует пределу увеличения угла гидродинамического сопротивления δH. Таким образом, следует ожидать уменьшение отношения VB / VT, но при достаточной силе ветра мощность парусов возрастает настолько, что достижимая максимальная скорость судна, напротив, увеличивается. Повышение восстанавливающего момента за счет приема водяного балласта или гидродинамической силы не лишено смысла, если речь идет о рекордных судах, рассчитанных на закрытую от волн акваторию; для открытого моря предпочтение нужно отдать простому устройству из двух крыльев Брюса.
Большинство парусников на подводных крыльях, построенных любителями, за малым исключением, не обнаружили преимущества в ходовых качествах перед обычными судами. Частично это объясняется завышенным весом н недостаточно продуманной конструкцией. В еще большей степени сказываются недостатки, вызванные слишком большими теоретическими упрощениями, принимаемыми при оценке подъемной силы подводных крыльев. Следует прежде всего принимать в расчет поправки па влияние свободной поверхности воды. Гидродинамическая подъемная сила определяется выражением
L = 1/2 · ρH VB2AFCL
| (6.12) |
где CL — коэффициент подъемной силы. Как было показано, CL линейно увеличивается с возрастанием угла атаки α вплоть до максимального значения. Наклон кривой можно принять численно равным 2π, если α выражено в радианах, или π2/90 ≈ 0,11, если α измерено в градусах для крыла бесконечного размаха в безграничной среде (влияние вязкости приводит к некоторому уменьшению коэффициента 2π, входящего в выражение (6.13) — прим. научн. ред.) Тогда
СL? = 2παT'
| (6.13) |
где αT — угол атаки, измеренный от пулевой подъемной силы. Величина наклона кривой СL описываемой уравнением (6.13), уменьшается в зависимости от ряда факторов.
В ограниченном потоке пониженное давление на верхней поверхности крыла не только создает подъемную силу, но и искажает свободную поверхность около него так, что разность давлений, а вместе с ней и подъемная сила уменьшаются. Искажение проявляется в виде образующейся волны. Этот эффект должен учитываться двумя поправками. Падение подъемной силы из-за уменьшения разности давлений может быть учтено умножением идеального коэффициента 2π иа величину
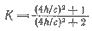
| (6.14) |
где h – величина заглубления крыла, с – хорда крыла.
Потеря подъемной силы составит около 5% при h/c = 1 н возрастает до 50% при h/c =0, когда крыло становится глиссирующей пластиной, для которой при бесконечном удлинении угол наклона кривой при бесконечном размахе равен π.
Влияние волнообразования может быть учтено поправкой
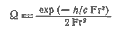
| (6.15) |
где Fг — число Фруда, взятое по хорде с,
Fr = VB / (gc)½
| (6.16) |
Значения этой функции для некоторых величин h/c приведены на графике (рис. 5.14), из которого видно, что пик кривых возник прн скорости судна VB = (2gh)½, что значительно ниже скорости выхода на крылья.
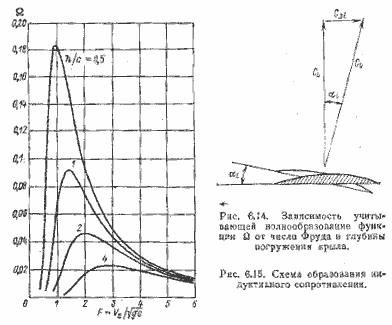
Итак, суда на подводных крыльях преодолевают горб волнового сопротивления на малой скорости, что является одним из их главных достоинств. Нужно заметить, что рассмотренная приближенная зависимость оказывается неприемлемой в случае движения судна на подводных крыльях по мелководью. Максимальная скорость движения гравитационной волны при глубине воды d равна (gd)½. Когда скорость судна превышает эту величину, характер волнообразования нарушается и для его объяснения требуется более сложная теория.
Подводное крыло конечного размаха (как к самолетное) испытывает падение подъемной силы н увеличение индуктивного сопротивления из-за действия систем вихрей, образующихся по боковым кромкам крыла. Для крыла эллиптической формы с относительным удлинением А индуктивные приращения угла атаки и сопротивления выражаются соотношением
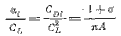
| (6.17) |
где б = 0 — для самолетного крыла и
б = A / (A + 12h/c)
| (6.18) |
для подводного крыла. Графически связь индуктивного сопротивления и угла атаки представлена на рис. 6.15. Физически названные потери связаны с затратами энергии на образование вихревых жгутов. Поправка, выражаемая формулой (6.18), вводится только при больших числах Фруда.
Для умеренных значений относительного удлинения может быть принят поправочный коэффициент, на который умножается идеальная величина наклона 2π кривой С1,
E = (1 + 2/A2)–1
| (6.19) |
Скорость потока, от которой зависит подъемная сила, направлена перпендикулярно размаху крыльев. Если используются крылья с углом стреловидности ф, результат (6.19) необходимо умножить на cos ф. Подобного же рода поправка необходима и для угла килеватости V-образного крыла. Угол атаки его в вертикальной плоскости, следовательно, должен быть уменьшен с учетом фактора сos Ф (Ф — угол килеватости крыла).
Определение относительного удлинения подводного крыла несколько сложнее, чем воздушного, из-за стоек, а также наличия границы раздела воздух – вода для крыльев, пересекающих поверхность воды.
На рис. 6.16, а показано горизонтальное подводное крыло с размахом в, поддерживаемое двумя стойками, установленными на расстоянии а одна от другой. С достаточным приближением эффективное удлинение этого крыл а может быть выражено уравнением
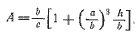
| (6.20) |
У крыльевых устройств с Т-образным профилем и одной вертикальной стойкой а –> 0 и A –> в/с. Для V-образных крыльев уравнение {6.20) можно преобразовать, нсходя из эквивалентной схемы, показанной пунктиром на рис. 6.16, б.
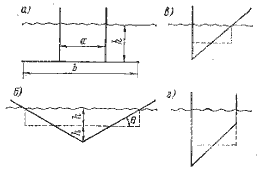
Рис. 6.16. К эквивалентности наклонных крыльев и горизонтальных крыльев с вертикальными стойками.
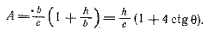
| (6.21) |
Так же можно получать ) выражения для асимметричных крыльевых устройств, изображенных на рис. 6.16 в, г. С учетом уравнений а (6.13)--(6.15), (6.17) и (6.19), коэффициент подъемной силы выразится
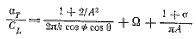
| (6.21) |
Только для больших чисел Фруда и высоких значений относительного удлинения при движении на глубокой воде это уравнение может быть заменено более простым
СL = 2π αF (A / (A + 2)
| (6.23) |
часто используемым в расчетах судостроителями-любителями (дополнительно отметим, что выражение (6.23) справедливо лишь для плоского нестреловидного крыла — прим. научн. ред.)
Коэффициент сопротивления крыла без учета вертикальных стоек равен
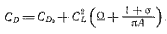
| (6.24) |
где СD, — коэффициент вязкостного сопротивления, который при отсутствии экспериментальных данных можно определить по формуле
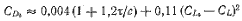
| (6.25) |
где т/с — отношение толщины профиля к хорде крыла. Сопротивление вертикальных стоек получается по формуле (6.25). Если стойки имеют обтекатели, которые не создают горизонтальной подъемной силы, то в правой части формулы (6.25) останется только один первый член. Место соединения крыльев со стойками является источником дополнительного сопротивления, величина которого в значительной мере зависит от плавности сопряженных обводов. Теперь, чтобы вознаградить практически мыслящего читателя, осилившего изложенный выше возможно и скучный, но очень необходимый материал, обратимся к вопросу о конструкции подводного крыла. Первая задача — выбор оптимального сечения. Для парусных судов с подводными крыльями, пересекающими свободную поверхность, по величине сопротивления наиболее приемлемым является профиль с острой носовой кромкой. Подобный профиль отличается равномерным распределением давления при малых углах атаки и, следовательно, не подвержен вентиляции. Крылья для проа, рассчитанного на достижение высоких скоростей, должны иметь аналогичный профиль, но заостренный одинаково с обеих сторон (например сегментный профиль с постоянным радиусом выпуклой поверхности) . Максимально возможная величина отношения для этого довольно простого профиля немногим меньше, чем для профиля с закругленной носовой кромкой (рис. 6.17).
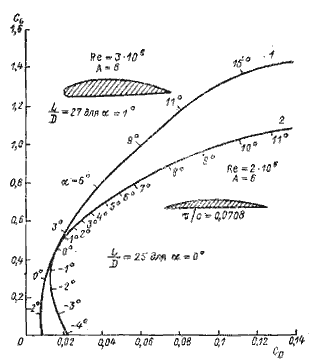
Рис. 6.17. Сравнительные характеристики профилей 1– NАСА 4415, 2 – Gö 708.
На практике это преимущество удается реализовать только при высококачественном изготовлении и шлифовке крыла, особенно в районе носовой кромки, что мало доступно для любительского изготовления.
Существует простая технология для изготовления крыла сегментного профиля. Основой приспособления служит многогранный равносторонний деревянный цилиндр с металлической тщательно отцентрированной осью. Плоские полосы-заготовки крыльев крепятся на каждой грани цилиндра и затем обтачиваются на токарном станке, как показано ва рис. 6.18.
Рис. 6.18. Приспособление для изготовления крыльев сегментного профиля.
Выбирая количество граней, можно получать желаемое отношение толщины профиля к его хорде, Например, чтобы изготовить крыло с профилем Gö 708 (разработан для планера), вужен цилиндр с 11 гранями. Для этого профиля отношение радиуса к хорде равно 1,7.
Подводные крылья можно изготовить из алюминиевых сплавов или ламинированного дерева, однако лучшим отношением прочности к весу обладает пенопласт, оклеенный после обработки стеклотканью или углетканью. Для повышения прочности могут быть установлены поперечные переборки из особо прочной ткани (рис. 5.19).
Рис. 6.19. Сечение сегментного крыла сэндвичевой конструкции (стеклоткань и пенопласт).
В этой главе основное внимание обращено на проблемы, вытекающие из высокой начальной остойчивости многокорпусных парусников. Следует отметить, что это качество нередко становится причиной аварий.
Многокорпусное судяо может потерять мачту в ситуации, при которой сжимающая мачту нагрузка на обычной яхте, не обладающей большой начальной остойчивостью, будет далека от предельной. В связи с высокой скоростью хода рули и шверты многокорпусных судов чаще ломаются. Эти особенности следует учитывать, проектируя судно. Опрокинутые вверх днищем многокорпусные суда столь же остойчивы, как и в положении на ровный киль, что порождает дополнительные проблемы.
Причинами опрокидывания судна может быть ветер, волна пли то н другое вместе. Как об этом говорилось в гл. 4, опрокидыванию препятствует большая ширина судна, низкое расположение центра тяжести и малое удлинение парусов, У тримаранов и проа эта зависимость несколько сложнее. Если подветренный поплавок ие обладает плавучестью, достаточной для поддержания на плаву всего судна. то начальная остойчивость уменьшается, а опасность опрокидывания быстро позрастает с погружением поплавка.
В экстремальных ситуациях можно ожидать, что обычное судно соскользнет по крутому склону волны и избежит опасной встречи с ее гребнем. Многокорпусные парусники с поплавками-аутригерами малой плавучести на такой маневр не способны, так как при крене на волне с погруженным подветренным аутригером обладают слишком большим боковым сопротивлением. В результате, погруженный поплавок как бы становится неподвижной осью, вокруг которой гребень волны опрокидывает судно. Шверт или шверцы на аутригере, увеличивающие его боковое сопротивление, должны быть в аварийной ситуации (при убранных парусах) подняты. Сказанное не относится к крыльям Брюса. Если угол наклона крыльев находится в рекомендованном пределе 40—45°, то при крене их плоскость оказывается параллельной поверхности воды и они, как водные лыжи, обеспечивают судну боковое скольжение. В меньшей степени это относится к ступенчатым крыльям. Об этом свидетельствует заслуживающий внимания опыт Д. Кейпера, который на своем крылатом тримаране Вилливо в очень суровых условиях прошел несколько тысяч миль по Тихому океану. остойчивость проа обеспечивается благодаря расположению главного корпуса всегда с наветренной стороны. При ветре переменных направлений судно может оказаться в обратной позиции. В этих условиях остойчивость проа меньше, чем у катамарана той же ширины. Во время своих первых плаваний на проа Чирс Т. Фоллет пережил опрокидывание, которое, к счастью, ограничилось 90° благодаря наличию имеющих достаточную плавучесть мачт на наветренном корпусе. Поставить судно на ровный киль своими силами ему, однако, не удалось. В качестве средства против опрокидывания Ньюик установил на наветренном борту спонсон, или буль (рис. 7.1), который должен задерживать опрокидывание при крене примерно 40°. С обезветренными парусами судно затем легко становится на ровный киль.
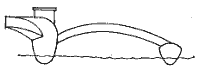
Рис. 7.1. Проа Чирс с наветренным спонсоном.
На крейсерских проа эту наделку можно использовать как дополнительный полезный объем. Гоночные суда, для которых обычно первостепенное значение имеют вес и парусность корпуса, вместо спонсона оборудуют надувным поплавком, который крепят к борту короткой балкой, превращая проа в разновидность тримарана. Другим решением проблемы опрокидывания для проа является применение устройства для автоматической отдачи шкотов, когда ветер заходит со стороны аутригера. Детали такого устройства изготовляются применительно к выбранному типу парусного вооружения; спроектировать их не представляет большого труда.
Шкоты на многокорпусных судах должны закладываться только в кулачковых стопорах, чтобы при необходимости их можно было мгновенно отдать. Пивер для своего тримарана сконструировал автоматическое устройство быстрой отдачи шкотов, показанное на рис. 7.2.
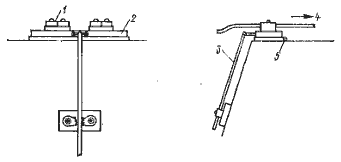
Рис. 7.2. Устройство дла автоматической отдачи шкотов конструкции Пивера.
1-- кулачковые стопора; 2— деревянные подушки; 3— эластичный трос; 4— шкот; S— ось вращения.
Оно состоит из одного или нескольких кулачковых стопоров, установленных иа планке, которая прикреплена к фундаменту на петлях со стороны паруса. Другая сторона планки фиксируется эластичной оттяжкой, заложенной в кулачковый стопор. Оттяжка отрегулирована так, что при определенном натяжении шкотов планка откидывается на петлях и шкот освобождается. Эффективность устройств быстрой отдачи шкотов зависит от степени свободы их закладывания. Очевидно, что многоходовые тали и системы лебедок для этой цели совершенно непригодны, Здесь удобен пирамидальный парус, который управляется одним шкотом и в силу своей сбалансированности не требует применения лебедок и других устройств, понижающих усилия. Достаточно установить в кокпите гребенчатый стопор.
Некоторые конструкторы для предотвращения полного опрокидывания считают целесообразным устанавливать на топе мачты дискообразный или каплеобразный поплавок. Я не нахожу эту идею плодотворной. Вес и парусность такого устройства лишь создают проблемы, которые оно же призвано решать. При опрокидывания динамическая нагрузка на топовый поплавок может оказаться столь значительной, что может сломать мачту. В результате, подобные устройства принесут болыше вреда, чем пользы.
В случае опрокидывания многокорпусное судно с большим объемом корпусов, такое, например, как Три Чирс (см. рис. 2.9}, будет обладать достаточно большой плавучестью. Для выхода экипажа следует предусматривать под одной из банок аварийный люк, который открывался бы в обе стороны. Такого рода аварийный люк ие годится для катамарана, наиболее целесообразно устраивать его на тримаране, в меньшей степени – на проа, У хорошо спроектированного тримарана боковые поплавки способны поддерживать судно на плаву даже после открытия аварийного люка, когда воздух из корпуса будет частично вытеснен водой. Для обеспечения безопасности экипажа на днище и по бортам должны быть предусмотрены леера-поручни. Кроме того, спасательный плот и припасы должны размещаться так, чтобы их можно было извлечь из опрокинутого вверх килем судна.
В течение ряда лет Ассоциация гоночных парусных яхт (AYRS) опубликовала несколько схем для постановки на ровный киль опрокинувшегося многокорпусного судна, но ни одна из них не применялась в практических условиях, не считая экспериментов, проведенных в закрытой гавани. Большинство из этих схем с незначительными видоизменениями основаны на методе, принцип которого показан на рис. 7.3.
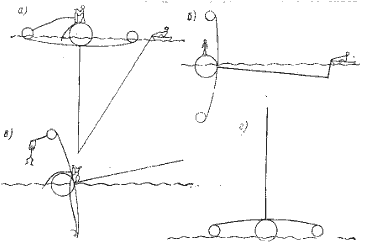
Рис. 7.3. Схема постановки на ровный киль опрокинувшегося тримарана.
В подветренный поплавок накачивают воду (рис. 7.3, а}, после чего со спасательного плота за фал мачту вытягивают из поверхность (рис. 7.3, б}. Судно выводят в положение с креном 90°. После этого выкачивают воду из погруженного поплавка (рис. 7.3, в), н под действием ветра и волн судно становится па ровный киль (рис. 7.3, г). Трудность заключается в затоплении подветренного поплавка, особенно если в его конструкции использован пенопласт. Только тримараны со шпоновыми поплавками и трубчатыми алюминиевыми поперечными балками могут быть поставлены таким способом на ровный киль и то, если при опрокидывании они не лишились мачты, что само по себе достаточно вероятно. Для катамаранов, а вообще н для проа, этот путь неприемлем.
Новая мысль в решении рассматриваемой задачи была высказана на Международном симпозиуме по многокорпусным яхтам в г. Торонто в 1976 г. С. Дж. Руисом из Сальвадора, предложившим проводить операцию по переворачиванию опрокинутого катамарана через нос. Опрокинутое судно, как показано на рис. 7.4, а, благодаря размешенным под крышей рубки блокам пенопласта имеет высокий надводный борт и сохраняет не залитой водой большую часть внутреннего объема (заштрихованные участки на чертеже показывают размещение пенопласта, вертикальная пунктирная линия — водонепроницаемую переборку, разделяющую рубку и носовой отсек).
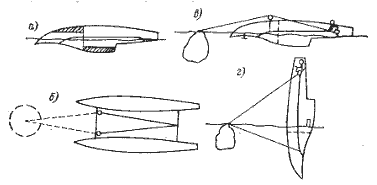
Рис. 7.4. Схема Руиса для постановки на ровный киль опрокинувшегося катамарана.
К передней поперечной балке со стороны днища прикреплена на петлях Л-образная балка из алюминиевых труб. К её вершине прикреплена мягкая емкость, которая заполняется водой, когда балка откидывается вперед (рис. 7.4, б).
Вторая Л-образная балка крепится вертикально на передней поперечной балке катамарана, а через блок на ее вершине пропускается привязанный к емкости линь, ходовой конец которого заведен на установленную в корме на днище мостика мощную лебедку (рис. 7.4, в). Далее, в палубе носовых оконечностей открываются клапана и по мере заполнения носовых отсеков водой и выбирания заведенного на заполненную водой емкость троса, катамаран погружается носом и занимает положение, показанное на рис. 7.4, г. Из окна рубки, которое в этом положении судна должно находиться чуть выше ватерлиния, выливается проникшая в нее вода. В этом положении катамаран сохраняет остойчивость, наподобие буя, но достаточно небольшого усилия на лебедке, и судно приходит на ровный киль. Большая часть воды, проникшей в боковые отсеки, благодаря плавучести, обеспечиваемой блоками пенопласта, выливается через клапана.
Следует обратить внимание, что применение этого способа не зависит от наличия мачты. При потере же мачты Л-образная балка после того, как катамаран займет нормальное положение, может служить аварийным рангоутом.
VB / VT = sin γ ctg β – cos γ
| (8.1) |
где γ и β — курсовые углы к направлению истинного и вымпельного ветра соответственно. Найдем скорость судна на различных углах γ в зависимости от скорости ветра VT, которые принимаются в качестве заданных известных переменных. Угол β представляет собой сумму углов аэро- и гидродинамического сопротивления бА и бН, равных
бА = arcctg (LА/DА), бН = arcctg (LН/DH)
| (8.2) |
Чтобы найти VB (или β), необходимо определить подъемную силу и сопротивление всех надводных и подводных частей судна. Рассмотрим это последовательно. Выражение для аэродинамической подъемной силы запишем
LА = 1/2 · pАVА2ASCLAcos2θ
| (8.3) |
Количество 1/2 · pА = 0,613 кг/м3.
Вымпельная скорость ветра VА может быть найдена через величины VB, VT и γ по теореме косинусов из треугольника скоростей (см. рис. 1.1)
VА2 = VB2 + VT2 + 2V VBVTcos γ
| (8.4) |
или через β, VT и γ согласно теореме синусов
VА / VT = sin γ / sin β
| (8.5) |
Площадь паруса AS можно рассматривать для двух предельных случаев: как некую постоянную при ветре от легкого до умеренного и как функцию величины 1/VА2 для свежего ветра, когда судно находится у предела своей поперечной остойчивости. В обонх случаях следует использовать уравнения остойчивости при различных типах парусного вооружения, выведенные в гл. 4.
Коэффициент подъемной силы почти линейно возрастает с увеличением угла атаки вплоть до его критического значения, равного для плоского паруса примерно 13°, а для выпуклого — 30. Когда углы атаки больше критического, подъемная сила уменьшается и при 90° равна нулю. Вид кривой зависит от удлинения паруса, его закручивания, наличия шайб, бортовой качки судна и многих других малых факторов, которые невозможно учесть в аналитических расчетах.
Последний член уравнения (8.3) – cos2θ учитывает крен. В случае пирамидального парусного вооружения cos2θ может быть заменен [cos2(θ + Ф) + cos2 (θ-Ф)] /2, где Ф — угол наклона пирамидального паруса (Ф = 19,5° для А = 3).
Аэродинамическое сопротивление рассчитывается по аналогичной формуле, за исключением добавки, которой учитывается сопротивление надводной части самого судна и различных устройств (рангоута, такелажа и т. д.),
DА = 1/2 pAVA2AS (CDA + εCPA)
| (8.6) |
Коэффициент сопротивления CDA включает составляющие сопротивлений трення, формы и индуктивного; в — отношение площади рангоута, стоячего такелажа, рубки и других элементов к площади паруса; CPA — соответствующий коэффициент сопротивления. Как в, так и CPA являются функциями β и угла крена. Конечное решение представляет сложную нелинейную зависимость, даже если имеются все необходимые данные. На рис. 8.1 приведена полярная диаграмма в координатах CLA и CDA для эффективного парусного вооружения при отсутствии на палубе рубки.
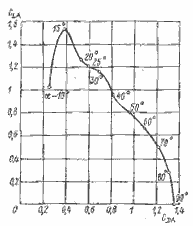
Рис. 8.1. Полярная диаграмма отношения подъемной силы к сопротивлению эффективного парусного вооружения.
Определение гидродинамической подъемной силы представляет собой не менее сложную задачу. Величина гидродинамической подъемной силы равна
LH = 1/2 pHVB2AP (APCLP + AKCLK
| (8.7) |
где ½pH = 513 кг/м3. Для того чтобы найти оптимальную площадь киля AK (ока может варьироваться), нужно приравнять LH к Fy, что еще более усложняет задачу. Расчеты DH= R также содержат много неопределенности. Как было показано в гл. 2, величина сопротивления зависит от многих условий. Хотя я питаю достаточно доверия к формуле Хавелока-Кейстла как инструменту для качественного анализа, нельзя ожидать, что получаемые с ее помощью количественные результаты будут во всех случаях приемлемы для любого типа судна, во всяких условиях плавания под парусами.
Однако эта сложная проблема может быль решена, например, методом последовательного приближения. Х. Майер в качестве первого приближения принимает некоторые значения углов дрейфа и крена, а также скорости судна для заданных γ и VT. Задавшись величиной VT, из треугольника скоростей получает β и VA. Значение VA подставляет в формулу остойчивости, для того чтобы найти уточненное значение ф = ф1. Решая совместно уравнения FX = DH и Fy = LH для найденных VA1 и β1, получает значение истинного ветра VT1 и уточненные значения угла дрейфа λ1 и скорости судна VB. Угол крена θ к скорость судна VB корректирует умножением на величину VT/VT1. Далее весь процесс повторяется до тех пор, пока отношение VT(n) к VT не приблизится к единице, а найденная VB не придет в соответствие с замеренной величиной. Метол вычислений, подобный изложенному, нельзя рассматривать в качестве общего принципа решения задачи; с его помощью можно получить ответы только на некоторые конкретные вопросы. Как можно было видеть на диаграмме рис. 1.7, буера ходят с углом β, близким к постоянному, до γ = 100°. Рассмотрим этот случай, характерный для быстроходных парусников. Выражение (8.1) можно записать
VB / VT = ψ sin γ – cos γ
| (8.8) |
где
ψ = ctg β = const
| (8.9) |
На рис. 8.2 приведена полярная диаграмма VB/VT в зависимости от γ для ряда β = const. Кривые представляют собой окружности радиусом
r = 1/2 · cosec β
| (8.9) |
Они проходят через нулевую точку и имеют центры на линии, заданной углом
γ = 90° + β
| (8.10) |
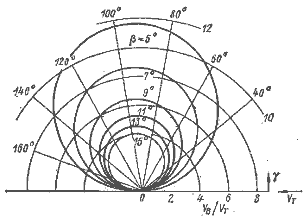
Рис. 8.2. Полярная диаграмма скорости хода в зависимости от курсового угла к истинному ветру при постоянном &beta.
Против ветра судно быстрее всего будет перемешаться при курсовом угле
YW45° + &beta / 2
| (8.12) |
развивая при этом скорость по генеральному курсу
VB/VT = 1/2 · (cosec β – 1)
| (8.13) |
Под ветер выгоднее идти с курсовым углом
YD135° + &beta / 2
| (8.14) |
Скорость по генеральному курсу будет
VB/VT · cos YD = 1/2 · (cosec β + 1)
| (8.15) |
Вывод уравнений (8.10) —(8.15) представлен в приложении. На рис. 8.3 изображена полярная диаграмма для буера при β = 6°. Ни одно другое парусное судно не ходит с постоянным β.
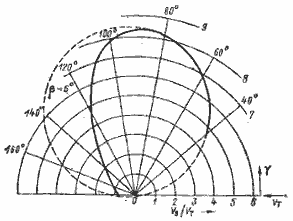
Рис. 8.3. Полярная диаграмма скоростей буера.
Анализируя ходовые качества менее быстроходных судов, будем исходить из равенства х-составляющих в векторном уравнении
FA = – FH
| (8.16) |
Заменив в формуле (2.23) R на DH = FA = 1/2 pAVA2AS CX и подставив значение VA2 в выражение (8.4), получим
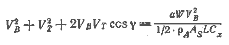
или
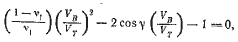
| (8.17) |
где
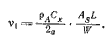
| (8.18) |
Уравнение (8.17) имеет решение
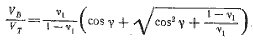
| (8.19) |
Чтобы уяснить физический смысл этого уравнения, нужно знать порядок величины vt. В интересующем нас диапазоне величина v1 обычно значительно меньше единицы. В этом пределе
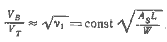
| (8.20) |
Согласно данным Келсела н Шатворта с точностью до 5% для VT= 10 уз можно приаять
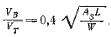
| (8.21) |
Формула (8.21) может быть использована для сравнения потенциальных ходовых качеств различных проектов.
Рассмотрим упрощенный вариант уравнения остойчивости для случая, когда наветренный корпус отрывается от воды,
yW = h (1/2 ρAVA2AS Cy)
| (8.22) |
Исключив с помощью выражения (8.1) VA2, получим
VB2 + 2VBVT cos γ + VT2 – v2 = 0
| (8.23) |
где
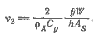
| (8.24) |
Уравнение (8.23) имеет решение
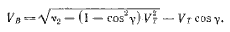
| (8.25) |
VB = (v2 – VT2)½
| (8.26) |
Это равенство показывает наибольшую скорость судна, которая достижима в галфвинд при ветре VT. Приняв Сн = 1 и исключив с помощью выражения (8.21) VT, определим максимально достижимую скорость в узлах
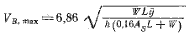
| (8.27) |
При проектировании судна, а также при разработке гоночных правил важно знать, как отражаются па ходовых качествах судна изменения отдельных характеристик (табл. 8.1).
Таблица 8.1. Характеристики некоторых английских многокорпусных парусников
| Название | W, кг | АS, м2 | Линейные размеры, м | VB / VT | Скорость, уз | |||
|---|---|---|---|---|---|---|---|---|
| L | h | y | VBmax | VT | Трайфл | 3600 | 75,0 | 12,1 | 6,4 | 4,1 | 0,803 | 27 | 33.6 |
| Ирокез 204 | 2935 | 43,0 | 8,3 | 4,1 | 2,0 | 0,557 | 21,7 | 33,6 |
| Крода уэй | 2734 | 57,4 | 9,8 | 5,2 | 3,7 | 0,725 | 26,4 | 36,4 |
| ФТ | 3492 | 75,6 | 8,4 | 5,5 | 4,0 | 0,684 | 254 | 37,1 |
| Таити Билл | 6211 | 81,4 | 11,2 | 6,4 | 2,5 | 0,613 | 22,2 | 36,2 |
| Три Чирс | 3769 | 89,6 | 13,2 | 6,6 | 4,0 | 0,896 | 25,3 | 29.4 |
| Г. Б. III | 19390 | 251,7 | 21,7 | 10,9 | 5,8 | 0,849 | 32,1 | 37,8 |
Правила IOMR, по которым проводятся гонки многокорпусных парусников, представляют номенклатуру показателей, которые достаточно полно характеризуют ходовые свойства яхт. Не включая обмеров общей ширины и длины аутригера, правила предоставляют конструкторам большую свободу выбора. К сожалению, они слишком сложны, чтобы стимулировать совершенствование конструкции. Келсел предложил заменить показатели, входящие в действующие правила IOMR, коэффициентом исправленного времени
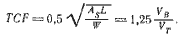
| (8.28) |
Для учета мореходных качеств целесообразно вводить поправку на ширину судна и возвышение центра парусности над центром бокового сопротивления корпуса, я гонок в слабый ветер имеет значение отношение площади парусов к площади смоченной поверхности, которое может быть учтено коэффициентом (AS/LB)½
Катамараны по ходовым качествам превосходят тримараны в свежий ветер, когда при отрыве одного корпуса от воды их сопротивление резко уменьшается. Это преимущество может быть реализовано на небольших, в основном гоночных судах, на которых команда, перемещаясь с борта на борт, создает дополнительный откренивающий момент, а возможное опрокидывание не влечет за собой серьезных последствий.
Таблица 9.1. Классификация гоночных катамаранов
| Класс | Габарит, фт | Порщадь парусности, фт2 |
Экипаж, чел. | |
|---|---|---|---|---|
| длина | ширина | |||
| A | 18 | 7,5 | 150 | 1 |
| B | 20 | 10 | 235 | 2 |
| C | 25 | 14 | 300 | 2 |
Гоночные катамараны делятся на три класса, которые различаются длиной, обшей шириной и площадью парусности (табл. 9.1). В дополнение к ним существует еще класс D (длина 30 фт, площадь паруса 500 фт2), который получил распространение только в Калифорнии. Наиболее широкую известность приобрели соревнования на катамаранах класса С. Это, прежде всего, периодически проводящиеся гонки на приз Малый кубок Америки. Катамараны типа Торнадо (класс В) конструкции Р. Марча включены в число парусных судов, на которых проводятся Олимпийские регаты. Все катамараны класса В имеют практически одинаковую конструкцию, не считая небольших отличий в рулях. Катамараны С относятся к свободному классу, именно в их конструкциях наблюдается наибольший прогресс, особенно в парусном вооружении.
Вначале на них устанавливалось вооружение тина шлюп, затем его заменили гротом. Скорость (одновременно и стоимость) катамаранов класса С стала быстро возрастать с появлением вращающейся мачты-крыла площадью до 50% общей площади паруса, мягкая часть которого снабжена сквозными латами. Последним шагом в этом направлении явилось полностью заменившее парус жесткое крыло, по внешнему виду напоминающее крыло планера. В слабый ветер подобные конструкции проигрывали из-за большого веса катамаранам с мягкими парусами, однако за счет применения различного рода суперсовременных материалов, вроде углепластика, баланс сил окончательно склонился в пользу жестких парусов. Для изменения профиля паруса-крыла на его задней жесткой кромке устанавливаются управляемые закрылки. Конструктор Д. Хаббард применил жесткий парус-крыло па катамаране Пейшнт Леди III, способный менять профиль в обоих направлениях. Это крыло имеет длину около 12 м и вес 104 кг‚ его передняя часть изготовлена из фанеры н углепластика. Паруса-крылья с изменяемым профилем доказали свою эффективность и на попутных курсах.
Что может быть дополнительно сказано о применении на парусных гоночных катамаранах подводных крыльев? Наиболее известные работы в этой области применительно к судам классов A и B выполнены Ф. Хенсфордом н Дж. Грогоно. Основой судна, на котором экспериментировал Грогоно, послужил серийный катамаран Торнадо. Крыльевое устройство, впервые установленное в конце 60-х годов, а затем многократно совершенствовавшееся, состоит из пары развитых кормовых и пары небольших носовых крыльев 9% -ного сегментного профиля, установленных с наклоном 45°. Управление осуществляется обычным рулем с удлиненным пером. Носовые крылья работают с углом атаки 4°, кормовые — 1°, что позволяет существенно демпфировать продольную качку (см. гл. 6). В дальнейшем размер крыльев был уменьшен, чтобы повысить скорость хода в крыльевом режиме и улучшить управляемость. Следующим усовершенствованием была подвеска носовых крыльев на петлях и использование их для управления судном.
Ф. Хенсфорд установил на катамаране класса А Мейфлай (см. рис. 6.11) крыльевое устройство самолетного типа. Основная нагрузка воспринимается передними крыльями, установленными по оконечностям поперечного бруса. Угол наклона крыльев 40°. Кормовое Т-образное крыло представляет собой единую конструкцию с пером руля. Крылья симметричного профиля установлены с нулевым углом атаки, что обеспечивает стабилизацию движения по глубине. Ширина поперечного бруса 14 фт (лишь немногим меньшая, чем длина судна) обеспечивает высокую поперечную остойчивость. Угол дрейфа саморегулируется благодаря возникающей на наветренном крыле отрицательной подъемной силе. Для придания судну большей продольной остойчивости носовые крылья были установлены под углом атаки 4, однако из-за неоптимального качества крылья оказались способны нести только 65% нагрузки. На высокой скорости, чтобы предотвратить носовой дифферент, рулевому приходится перемещаться к самой корме. На Мейфлае были показаны феноменальные результаты. В 1972 г. во время заездов на побитие рекорда скорости под парусами в Веймутском заливе катамаран показал скорость 16,4 уз. В 1975г. ту же 500-метровую дистанцию Мейфлай прошел со скоростью 19,4 уз, а в 1977 г. повысил это достижение и рекорд в классе А до 21,2 уз.
Икарус по сравнению с Мейфлаем нмеет меньшую ходовую поперечную остойчивость, но и угол дрейфа у него меньше. В идеальных условиях Икарус развивал скорость до 26 уз, однако на официальных заездах в Веймутском заливе он прошел дистанцию медленнее, чем Мейфлай, развив скорость 20,7 уз, На этих соревнованиях у Икаруса было крыльевое устройство, такого же типа, как и у Мейфлая. Причиной, помешавшей ему развить более высокую скорость, были большие, чем у Мейфлая, вес в величина ходового крена (вес Мейфлая без рулевого всего 130—150ф!). На катамаранах более крупных размеров, пригодных для плавания в удалении от берегов, при общей длине более 40 фт, как правило, в корпусах и на мостике оборудуются жилые помещения. Для крейсерских гонок с экипажами из одного или двух человек катамараны не столь популярны, как тримараны. Катамараны строятся с гибкими или жесткими поперечными связями. Средн быстроходных «жестких» катамаранов можно назвать Сисмоук и Таити Билл. По современным стандартам, они слишком тяжелы (первый длиной по ватерлинии 15,07 м имеет водоизмещение 11,09 т, второй на 3 м короче и его водоизмещение 6,21 т) и узки. Дж. Уоррем спроектировал ряд «гибких» крейсерских катамаранов, продемонстрировавших хорошие мореходные качества.
Менее удачны оказались гоночные суда. Проектируя катамаран Мироркэт, предназначавшийся для гонок вокруг Великобритании, Мак-Альпин-Доуни взял за основу два 40-футовых корпуса Команча и соединил их трубами из алюминиевых сплавов. Все оборудование состоит из натянутого между поперечными балками и корпусами тента. В гонках судно оказалось неконкурентоспособным и после усиления конструкции стало использоваться для крейсерских плаваний. Другой катамаран, построенный по проекту Мак-Альпин-Доуни, Бритиш Оксиген, представляет собой увеличенную до 21,3 м модель Торнадо. Конструкция его с четырьмя поперечными трубчатыми связями из легкого сплава рассчитывалась методами, применяемыми в английской авиапромышленности. В 1974 г. сразу же после постройки он занял первое место на гонке вокруг Британии, опередив, хотя и незначительно, 46-футовый тримаран Три Чирс. Переименованное в Крайтер III судно потерпело аварию во время шторма в 1976 г., встретившего в Северной Атлантике участников трансокеанской гонки одиночек. От удара гигантской волны сломалась сначала носовая балка, а затем одна за другой и остальные. Рулевой Жак-Ив Терлен был снят с судна за миг до того, как оно пошло ко дну.
На тримаранах мачта устанавливается на главном корпусе, а на катамаранах — на середине пролета поперечной связи. Мачта, штаги и ванты под ветровой нагрузкой создают значительные напряжения в конструкциях моста, с учетом которых приходится увеличивать прочность (а следовательно, и вес) связей,ограничивать ширину судна. По этой причине типы саморазгружающегося парусного вооружения, подобные пирамидальному, для катамаранов еще более перспективны, чем для тримаранов. Рассмотрим вопрос прочности поперечных связей более подробно.
В гл. 3 установлено, что изгибающие напряжения для поперечных связей представляют наибольшую опасность. Максимально допустимое напряжение было определено в (3.1) зависимостью
бmax = Wlh/I,
| (9.1) |
в которой W — вес судна; l — длина поперечной балки, h — половина высоты балки, I — момент инерции площади поперечного сечения, который для пустотелой балки прямоугольного сечения равен
I = 2/3 · a [h3 - (h - τ)3]
| (9.2) |
где а – ширина балки; т – толщина стенок балки. При достаточно большой площади поперечного сечения h >> т уравнение (9.2) упрощается
I ≈ 2ah2τ
| (9.3) |
а (9.1) может быть записано
бmax = 1/2 · Wl/ahτ
| (9.4) |
Вес поперечной балки, которую мы принимаем сужающейся по высоте на конус, приближенно равен
WB = l (a + 2h) τv
| (9.5) |
где v — удельный вес материала балки. Исключим с помощью уравнений (9.4) величину т из формулы (9.5)
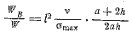
| (9.6) |
отсюда находим длину балки
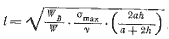
| (9.7) |
Величина бmax/v полностью зависит от материала, из которого сделаны балки. Величина в скобках нмеет размерность длины и учитывает геометрический фактор. Так как при подобии судов геометрический фактор принимается пропорциональным L, длина поперечной балки может увеличиваться соразмерно L½.
Катамараны должны проектироваться так, чтобы в полную меру использовались нх преимущества перед тримаранами, в частности меньшая парусность корпуса, а следовательно, лучшая маневренность. Использование пирамидального парусного вооружения обеспечивает выигрыш в весе по сравнению с тримаранам тех же размерений и снижает отношение наибольшей длины к полной ширине катамарана, которое чаще всего выражается как 2:1. Возрастание при этом величины (ASL/W)½ обеспечивает повышение предела достижимой скорости. Проект подобного судна приведен на рис. 9.1. Его основные размеры: L = 24,4 м, B = 14 м, W = 10 т.
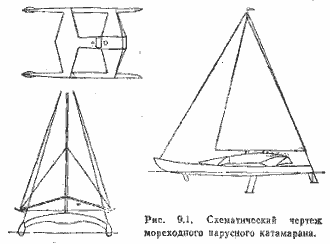
Рис. 9.1. Схематический чертеж мореходного парусного катамарана.
Проектом, в зависимости от размерений, предусматривается размещение на мостике оборудования для экипажа от 1 до 3 чел. Боковое сопротивление обеспечивается гидравлически управляемыми швертами, подвешенными на внутренних бортах корпусов. Паруса с относительным удлинением около четырех имеют по нижней шкаторине аэродинамические шайбы. В настоящее время на таком судне подводные крылья не применяются. Для 50-футового катамарана они не дадут преимущества при скорости менее 20 уз, но, в связи с тем, что прогресс в этой области не остановился, вопрос остается открытым.
Рассмотрим преимущества тримаранов перед катамаранами. На рис. 10.1, а дана схема поперечного сечения тримарана, на которой показана концентрация нагрузки в главном корпусе.
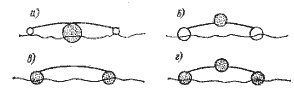
Рис. 10.1. Поперечное распределение нагрузки; а — тримарана; б, в, г — катамаранов.
В некоторых проектах аутригеры используются в качестве грузовых помещений, однако такие суда нс могут быть отнесены к высокоскоростным и поэтому ие рассматриваются. На рис. 10.1 б,в,г показаны три возможных варианта расположения грузовых помещений на катамаранах. Малые катамараны несут вссь груз на мостике (рис. 10.1,6), поэтому центр тяжести у них располагается высоко (большая величина z), что отрицательно влияет на боковую остойчивость. На рис. 10.1, в показан катамаран, грузовые помещения которого расположены в корпусах (например, Мирроркэт). К сожалению, поперечные связи таких катамаранов не обладают достаточной жесткостью. Наконец последний вариант (рис. 10.1, г), используют под нагрузку как корпуса, так и просторную рубку на мостике (Сисмоук). Подобные конструкции отличаются высокой прочностью, во имеют слишком большое водоизмещение с полным грузом. Преимуществами тримаранов являются низкое положение центра тяжести (малая величина z) и малый момент инерции относительно продольной оси. Последнее способствует снижению резкости бортовой качки при достаточно высокой остойчивости, обеспечиваемой значительной шириной поперечного мостика.
Тримараны благодаря развитым носовому н кормовому свесам основного корпуса, а также отрыву наветренного корпуса от воды легче лавируют. В слабый ветер на фордевинде тримаран может ходить практически на одном главном корпусе, сопротивление поплавков в этих случаях пренебрежимо мало. В слабый ветер скорость хода такова, что суммарное сопротивление воды движению судна в основном зависит от сопротивления трения, а следовательно, от смоченной поверхности корпусов. Смоченная поверхность судна, состоящая из нескольких корпусов, имеющих одинаковые длину и призматический коэффициент, увеличивается пропорционально корню квадратному от числа корпусов, находящихся в воде, Это нетрудно показать с помощью уравнений (2.20) и (2.22), которые для данного случая могут быть записаны в виде
AW = nc1B
| (10.1) |
c2 = nB2
| (10.2) |
где c1 и c2 — постоянные, а n -— количество корпусов. Исключив величину В — ширину каждого отдельного корпуса — путем совместного решения уравнений (10.1) и (10.2), получим
AW = c1(c2)n½
| (10.3) |
что соответствует сказанному выше, Следовательно, катамаран может иметь преимущество только при отрыве одного корпуса от воды, что близко к пределу его остойчивости. В общем случае проблемы прочности тримарана решаются проще, чем катамарана, уже потому, что нагрузка у него сосредоточена в главном корпусе, а не распределена, как у катамарана, по корпусам н мостику. Поэтому, как н на обычном судне, на тримаране один руль и вспомогательный двигатель установлен там же.
Сравнительно короткие поперечные связи тримарана позволяют обеспечить вертикальный клиренс, исключающий замывание днища мостика. На катамаране величина клиренса ограничивается необходимостью располагать на мостике помещения, выдерживая приемлемую величину парусности корпуса. Преимущества катамарана — малые вес и парусность корпуса — в полной мере удается реализовать только на очень больших судах. Применяя сверхпрочные н легкие материалы для мостика и корпусов, можно достичь величины DLR = 20, обеспечив при этом необходимую прочность. Тримараны длиной менее 21 м получают преимущество перед катамаранами, которое становится особенно заметным при L = 15 м, но при L = 9 м катамараны снова становятся более перспективными, Исходя из сказанного, постройка гоночных катамаранов с гибкими поперечными связями нецелесообразна (по крайней мере наиболее крупных судов этого типа), так как их прочность не может быть обеспечена в достаточной мере. В гл. 9 установлена зависимость (9.7) ширины катамарана от L½. Для гоночных тримаранов с корпусами, выполненными из стеклопластика, приближенно можно принять
DLR = 200 / L½
| (10.4) |
откуда вес в фунтах будет выражен
W = 0,5 L2,5
| (10.5) |
Данная конструкция является оптимальной для гоночных судов не столько оттого, что она позволяет получить лучшее соотношение прочности н веса, но, прежде всего, из-за большой величины отношения жесткости к весу, которая гарантирует тугую натяжку штага. Наилучшие характеристики по прочности и весу обеспечивают сэндвичевые (с применением пенопласта) конструкция, снабженные пирамидальным парусом. На тримаранах для аутригеров и поперечных связей применяется углепластик. Установим зависимость между размерами и скоростью судна. Приняв, согласно (9.7), что общая ширина судна при пропорциональном увеличении сечения поперечных связей возрастает в масштабе L½, а вес — в масштабе 2,5, получим, что отношение Vл / VT в выражении (8.20) будет изменяться как L½. При этом максимальная скорость (8.27) останется почти постоянной. Если же сечение поперечных связей будет увеличиваться быстрее, чем L2 то возрастание общей ширины будет линейным, веса — как L3, отношение Vл / VT станет почти постоянным, а предел скорости будет расти как L½. В качестве примера на рис. 10.2 приведены чертежи общего вида тримарана 50-футового класса. Его основные размеры: L = 17,7 м, В = 10 м, W = 3,27 т.
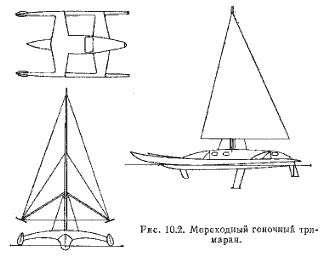
Рис. 10.2. Мореходный гоночный тримаран.
Рассмотрим применение подводных крыльев на тримаранах для открытого моря. Приемлемы обе классические схемы расположения крыльев — самолетная и типа «утка». Опыт свидетельствует, что переднее крыло в схеме «утка» несет около 15% нагрузки, остальные 85% приходятся на два задних Брюсовых крыла. При этом больший угол атаки носового крыла, н, как следствие, отношение L/D ниже оптимального лишь незначительно ухудшает гидродинамическое качество системы. Аутригеры тримаранов на подводных крыльях имеют меньшие размеры. Однако необходимо, чтобы до выхода на крылья величина DLR не достигала значения, при котором волновое сопротивление становится пиковым. Крылья устанавливают так, чтобы носовое выходило на режим первым. Это увеличивает угол атаки основных крыльев и ускоряет выход корпуса судна из воды, Ось, вокруг которой судно совершает продольные колебания, сдвинута от миделя к носовой оконечности. Для надежной работы носового крыла важно предусмотреть в шторм резерв плошади вблизи ватерлинии.
Благодаря удачному распределению нагрузки и высокой остойчивости схема «утка» представляется гидродинамически более эффективной, чем самолетная. Достижения, показанные на катамаране Мейфлай, говорят об обратном. Самолетная схема использована в проекте 69-футового тримарана Пан Дюнк VII (рис. 10.3).
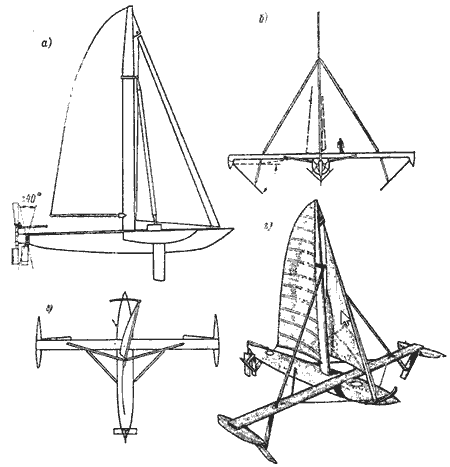
Рис. 10.3. Тримаран Пан Дюик VII: а - боковой вид; б - вид спереди; в - вид сверху; г - общий вид.
Конструкция из профилированного алюминия максимально облегчена. Полный проектный вес судна составил 5488 кг. Размах поперечного бруса, несущего два передних крыла, 20,1 м, т. е. на 2,1 м больше длины корпуса. Эти крылья можно установить с наклоном до 45° так, чтобы обеспечить при положении на ровный киль почти полное отсутствие кренящего момента. Они несут около 65% нагрузки, остальные 35% приходятся на кормовое крыло, которое служит одновременно рулем и средством для удифферентовки.
Тримаран оснащен парусным вооружением шлюп площадью 200 м2. Поворотная мачта (18 м) не имеет вант, а раскреплена двумя трубчатыми стойками, опирающимися на поперечный брус. Это необычное крепление является причиной того, что мачта больше работает на растяжение, чем на сжатие. Испытания модели тримарана показали, что он будет выходить ва крыло при скорости 12 уз, после чего без особых дополнительных усилий сможет разогнаться до 20—25 уз. Э. Табарли предполагал, что судно сможет пересечь Атлантический океан за 15 сут. (Этот прогноз не только подтвердился, но и был превзойден. В 1981 г. Табарли пересек Атлантический океан за 10 сут 5 ч 14 мин. Рекорд был установлен на тримаране Поль Рикар, у которого крылья служили только для откренивания и удифферентовки судна. Пан Дюик VII так и не был построен из-за непреодолимых трудностей при воплощении конструктивных решений. Прим. перев.)
К моменту написания книги (1979 г.) единственное парусное судно на подводных крыльях (тримаран Вилливо Д. Кейпера) пересекло океан. Вилливо имеет длину 9,5 м и полный вес 953 кг, из которых 181 кг приходится аа крыльевую систему, изготовленную из алюминиевых сплавов. Судно несет парусное вооружение типа шлюп площадью 35,3 м2. Крыльевое устройство нельзя отнести ни к типу «утка», ни к самолетному, ово состоит из четырех крыльев. На фото (рис. 10.4) Вилливо показан с поднятыми крыльями.

Рис. 10.4. Тримаран Вилливо с поднятыми крыльями.
Аутригеры малого размера впоследствии для откренивания были заменены большими. Носовое крыло c хордой 15 см имеет размах, равный ширине тримарана. Минимальный утол наклона 30°. Кормовое трехступенчатое крыло служит одновременно и рулем. Бортовые четырехступенчатые крылья устанавливаются с наклоном 35°. Ходовой крен не превышает 5-10°, при этом наветренное крыло выходит нз воды н восстанавливающий момент достигает наибольшей величины.
Вилливо спроектирован в 1963 г., построен в 1966 г. В 1969 г. тримаран впервые испытан в открытом море, а в 1970 г. на нем совершен 16-дневный переход в очень свежую погоду из Сауселито (Калифорния) до острова Мауи (Гавайи).

Рис. 10.5. Тримаран Вилливо на крыльях в океане.
Следующим был рейс протяженностью 20 тыс. миль от Калифорнии через Тихий очеая ло Новой Зеландии. Вилливо выходит на крылья, когда его скорость достигает 12 уз, а скорость ветра – более 13 уз. Ирк этом площадь горизонтальной проекции крыльев составляет около 1,1 м2. Аутригеры первоначальной конструкции имели водоизмещение по 270 кг. Учитывая возможность внезапных сильных порывов ветра, конструктор в дальнейшем увеличил его до 900 кг. Носовое крыло имеет угол стреловидности по передней кромке равный 10°, а бортовые крылья — 14°. Поэтому на большой скорости вода поднимается по стойкам крыльев, предотвращая их вентиляцию. С той же целью на стыке стоек и крыльев размещены каплеобразные наделки. В идеальных условиях Вилливо развивает скорость более 20 уз. Дальние плавания совершались с малым скоростями, но в них судно проявило отличные мореходные качества и подтвердило перспективность принятой схемы крыльевого устройства для плавания под парусом в открытом море (рис. 10.5).
Как тип парусного спортивного судна проа известно в меньшей степени, чем другие многокорпусные суда. По этон причине использование современных материалов и технологий не оказало столь значительного влияния на их конструкцию, какое имело место для катамаранов и тримаранов. Летучие проа ведут своё происхождение от судов, строившихся в Микронезии и, с особенно большим искусством, на Марианских островах в ХIV—ХV вв. Они имели длину 70 и более футов и в благоприятных условиях развивали скорость до 20 уз, неся тканые, наподобие циновок, паруса. Во время испанской колонизации островов проа использовались для почтовых перевозок между Каролинскими, Марианскими и Филиппинскими островами. Рассказывают, на одном из них за 6 дней был совершен переход из Гуама в Манилу протяженностью 1700 миль.
Представление о микронезийском летучем проа дает чертеж (рис. 11.1), построенный на основе исторических источников и данных, полученных от профессора Техасского университета Е. Дорана.
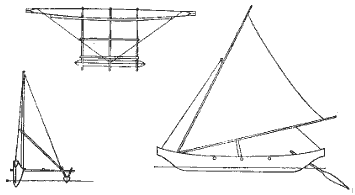
Рис. 11.1. Микронезийское летучее проа.
Главный корлус имеет асимметричные обводы, более выпуклый борт обращен в наветренную сторону. В качестве аутригера использовано цельное бревно с небольшим запасом плавучести. Судно ходит, всегда имея аутригер с наветренной стороны. Если аутригер окажется с подветренной стороны, то достаточно легкого порыва ветра, чтобы бревно-поплавок погрузилось в воду и судно опрокинулось. Управляется летучее проа многочисленным н очень подвижным экипажем, который, перемещаясь по поперечным балкам аутригера, откренивает судно так. чтобы поплавок скользил над водой совсем близко от ее поверхности (отсюда и название).
Использование проа в качестве спортивных судов, обычно имеющих небольшой экипаж, потребовало внести изменения в традиционную конструкцию. Первый шаг в этом направлении сделал Д. Ньюик, построивший в 1967 г. проа Чирс. Основной корпус судна, на котором размещено оборудование, включая двухмачтовое парусное вооружение типа шхуна, руль и шверт, располагается в отличие от летучего проа неё с подветренной, а с наветренной стороны. Подветренный корпус Чирса водоизмещением наполовину меньше наветренного обеспечивает поперечную остойчивость за счет подъемной силы, увеличивающейся по мере его погружения в воду. Чирс проявил себя надежным н быстроходным судном: в трансатлантической гонке яхт-одиночек OSTAR-68 он финишировал третьим. Конструкция Чирса с аутригером-поплавком на подветренной стороне послужила основой для развития нового типа проа, названного «атлантическим». Два таких судна Сайдвиндер и Лиллиан, построенные вскоре после Чирса Келселом, не принесли, однако, их конструктору успеха. Установка шверцев на аутригере Сайдвиндера вызвала затруднения с центровкой. Повторение двухмачтового варианта парусного вооружения также’ оказалось не слишком удачным: из-за близкого расположения одного от другого передний парус задувал в грот, уменьшая эффективность его работы.
Развитие конструкции атлантических проа привело к использованию подводных крыльев на поплавке-аутригере для увеличения его подъемной силы и снижения сопротивления. Впервые эта идея была реализована Дж. Чепменом, построившим в 1972 г. 5,5-метровое проа на подводных крыльях Тайгер. На нем, как и на Чирсе, эклпаж и все оборудование размещаются в главном наветренном корпусе. Два крыла на метровых стойках установлены по оконечностям поперечных трубчатых балок. Поллавок-аутригер из фанеры с пенопластовым заполнителем обладает минимальной плавучестью, обеспечивающей остойчивость на малой скорости. Единственный парус Тайгера поднимается ва установленной в плоскости миделя поворотной мачте (рис. 11.2).
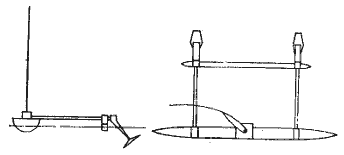
Рис. 11.2. Проа Тайгер.
У Тайгера оказалась очень плохая центровка. При установке носового крыла с углом атаки 5°, а кормового 4° устойчивость движения обеспечивалась только на курсе, близком к галфвинду. На более крутых курсах (рис. 11.3) судно приводилось, а на полных — уваливалось под ветер.
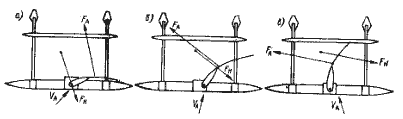
Рис. 11.3. Недостаток устойчивости на курсе проа атлантического типа: а – бейдевинд (судно приводится на ветер); б – курс, близкий к галфвинду (устойчивость обеспечена); в – бакштаг (судно уваливается под ветер).
При снятых крыльях и установленных на наветренном (главном) корпусе шверцах удовлетворительная центровка была получена в широком диапазоне курсовых углов.
Оптимальность такого решения подтверждается н опытом плавания Чирса, имеющего хорошую центровку. Рассмотрим вопрос о центровке праз более подробно. На рис. 11.4 дана схема сил, действующих на судно в вертикальной плоскости.
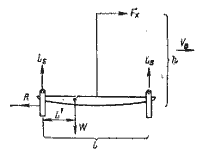
Рис. 11.4. Силы и моменты, действующие на проа в продольной плоскости.
Из условия равновесия сил можна записать
Fx = R
| (11.1) |
LS + LB= W
| (11.1) |
причем в равенстве (11.1) принято допущение, что судно идет в положении, близком к пределу боковой остойчивости, при котором сопротивление наветренного корпуса как пренебрежимо малое не учитывается. Из равенства нулю дифферентующих моментов относительно кормового крыла получим
Fxh + WL' = LBL
| (11.3) |
На схеме проа в плане (онс. 11.5) видно, что центр парусности находится на расстояниях b и l, соответственно к ветру и в нос от кормового крыла.
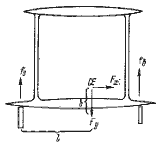
Рис. 11.5. Силы и моменты, действующие в горизонтальной плоскости. Запишем еще два уравнения
IS + IB = Fy
| (11.4) |
IBL = Fxb + FyL
| (11.5) |
Для V-образных подводных крыльев с фиксированным углом килеватости (потенциальные возможности крыльев с переменной килеватостью представляются бесперспективными для малых судов)
IB, S = LB, S tg θ
| (11.6) |
Fy = W tg θ
| (11.7) |
Чтобы решить эти уравнения, необходима еще одна зависимость. Согласно рис. 6.1, в достаточно широком диапазоне скоростей для судов на подводных крыльях можно принять, что
Fx = R ≈ 1/7 W
| (11.8) |
Из приведенных уравнений находим величину l, характеризующую положение центра парусности по длине судна,
l = L' + 1/7 (h – b ctg θ
| (11.9) |
и определяем подъемную силу носового и кормового крыльев
LB = W/L · (L' + h/7)
| (11.10) |
LS = W/L · (L – L' – h/7)
| (11.11) |
Что из этого следует? Для небольших проа за счет перемещения экипажа в корму (L' < L/2) центр парусности может быть сдвинут от миделя в корму. Если, напротив, требуется, чтобы центр тяжести находился на миделе (L' = L/2), как это имеет место на больших проа, то для h > В ctg θ, что необходимо для центровки в широком диапазоне курсовых углов, находим l > L / 2, т. е. центр парусности должен находиться в нос от миделя. Этот факт должен учитываться при проектировании парусного вооружения. При простейшем парусном вооружения проа мачта устанавливается у миделя (рис. 11.6).
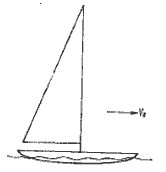
Простейшее парусное вооружение проа.
Однако центр парусности при этом всегда будет смещен в корму. Для того чтобы иметь возможность регулировать центровку, используют подвижные мачты. Такая конструкция применена при модернизации в 1973 г. проа Тайгер, Новое парусное вооружение, установленное на подветренном борту, превратило судно из атлантического в тихоокеанское проа. В таком виде оно лучше управлялось, чему в немалой степени способствовало устройство для перемещения мачты, состоящее нз проложенного дугой вдоль борта рельса, по которому перемещался шпор мачты. Для выполнения поворота проа становится лагом к ветру с растравленными шкотами, и мачта оттягивается по рельсу к миделю. В таком положения судно остается, пока рулевое управление не перенесут с кормы на нос и не изменят соответствующим образом углы атаки подводных крыльев. Затем шпор мачты передвигают дальше к оконечности, которая стала носовой, подбирают шкоты, и проа ложится на новый галс.
Недостатком этой системы является сложность выполнения маневра. Для более крупных проа она вообще не применима. Паруса с большим удлинением или малой плошади не позволят перенести центр парусности достаточно далеко вперед, чтобы обеспечить центровку на судне с центром тяжести у миделя.
На рис. 11.7 показано парусное вооружение, разработанное в 1962 г. Дж. Тейлором. Парус имеет конфигурацию равнобедренного треугольника. Оба нижних угла снабжены шкотами, проведенными на мощные лебедки. Выбранный втугую шкот в носу исполняет роль штага, кормовым шкотом настраивается положение паруса к ветру, При повороте функции такелажа, так же как положение кормы и носа, меняются. В обоих случаях обеспечивается носовая центровка паруса и сбалансированность аэродинамических и гидродинамических сил. Как и любое стаксельное вооружение, этот парус создает значительные нагрузки на корпус судна.
Из вышеизложенного следует, что пирамидальные паруса предпочтительнее для больших проа. Вес рангоута, конечно, получается больше, чем при вооружении, примененном Тейлором, однако меньшая величина усилий, передаваемых на корпусные связи, дает возможность получить выигрыш в суммарном весе судна. Паруса, установленные симметрично относительно миделя и на достаточно большом расстоянии друг от друга, позволяют изменять центровку в широких пределах. Они могут иметь большое удлинение, обеспечивающее высокое аэродинамическое качество, без излишне высоких мачт. Центровка не нарушается и при различных вариантах рифления парусов. Высокоэффективные паруса и подводные крылья дают возможность иметь хорошую устойчивость на курсе при высокой скорости хода. Оптимальное поперечное расположение парусного вооружения (лучшая поперечная центровка) достигается в том случае, когда цевтр давления ветра располагается над линией действия результирующей силы гидродинамического сопротивления. Поскольку для быстроходного проа это условие должно соблюдаться при уменьшенном сопротивлении наветренного корпуса, центр давления паруса должен быть смещен к подветренному корпусу. По этой причине при установке подводных крыльев предпочтителен тихоокеанский вариант проа, а для судов тнпа Чирс — атлантический.
Нужно отметить, что судно идет без крена при любом размещении парусов по его ширине до тех пор, пока линия действия гидродинамических сил подводных крыльев пересекается с линией силы тяги парусов над центром тяжести. Именно это условие удовлетворяет уравнению (6.7): прохождение гидродинамической силы крыльев через центр давления на парусе не является обязательным.
Главным качеством любой мореходной конструкции является простота. Согласно этой концепции подводные крылья со стойками надо крепить к корпусу с учетом нх полного подъема. Для того чтобы в многоступенчатой крыльевой системе носовое крыло имело большую подъемную силу, чем кормовое, при любом направлении движения нижние плоскости того и другого устанавливаются с нулевым углом атаки, вторые плоскости носового — с углом атаки +1,3°, кормового –1,3°; третьи соответственно + 2,6° и –2.6° и верхние +4° и –4°. Такое расположение крыльев обеспечивает носовому крылу значительную подъемную силу на любом курсе без дополнительной регулировки при выполнении поворота. В случае возникновения дифферента на нос подъемная сила кормовых крыльев уменьшается быстрее, чем носовых, и положение на ровный киль восстанавливается автоматически. Управляемость проа обеспечивается системой, описанной в конце гл. 5. На проа с подводными крыльями руль подвешивается к стойке крыла, как показано на рис. 11.8.
Рис. 11.8 Совмещение руля со ступенчатым подводным крылом.
Поскольку крылья могут быть подняты при плавании на мелководье или в слабый ветер, желательно управлять рулем с помощыо гидропривода (рис. 5.11). Результат приведенных выше рассуждений представлен на рис. 11.9 в виде схематического чертежа проа для плавания в открытом море.
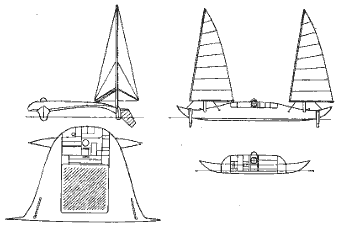
Рис. 11.9. Мореходное проа на подводных крыльях. Парусное вооружение – шхуна.
На любом курсе, кроме чистого фордевинда, скорость парусного судна относительно истинного ветра определяется величиной угла β между векторами скоростей судна и вымпельного ветра. Чем меньше угол β, тем быстроходнее судно. Согласно теореме курсов (1.5) β может быть представлен суммой углов аэро- и гидродинамического сопротивления, которые зависят от отношения подъемной снлы к сопротивлению соответственно надводной и подводной частей судна. При создании быстроходного парусного судна необходимо стремиться достичь возможно большей величины этих отношений, обеспечить приемлемые мореходные качества и условия для экипажа. Угол гидродинамического сопротивления любого парусного судна {исключая буер) намного превышает угол газодинамического сопротивления практически па всех курсовых углах. Важно знать пути уменьшения сопротивления воды движению судна при заданных нагрузках. Работы Хавелока — Кейстла позволили установить, что корпуса и аутригеры следует проектировать с возможно большим призматическим коэффициентом и оконечностями, не создающими при движении завихрений. Практически установлено, что заострение 14° на каждый борт близко к оптимальному. При соблюдении этого условия и высоком значении отношения длины к ширине корпуса большая величина призматического коэффициента достигается сама собой.
Мои рекомендации по поводу аутригеров тримаранов отличны от общепринятых. В настоящее время одни конструкторы отдают предпочтение аутригерам с большой плавучестью, другие —с малой (полностью погружающиеся аутригеры). В связи с тем, что подветренный аутригер воспринимает значительную часть общей нагрузки на острых к ветру курсах, для снижения сопротивления целесообразно проектировать аутригеры с большой плавучестью, но с возможно меньшим значением отношения водоизмещения к длине (насколько это доступно), учитывая величину нагрузки и качество применяемых материалов. В общем, аутригеры должны иметь несколько большую длину, чем корпус.
Современное состояние судостроения, включая материалы, позволяет создавать легкие высокопрочные конструкции. Проектируя многокорпусные парусники, необходимо учитывать, что их поперечные связи, рули, крылья, шверты испытывают напряжения, каких не бывает на обычных яхтах. Этим объясняется стремление освоить для постройки таких судов материалы, не находящие применения в яхтостроении, например углепластики. Минимальный угол аэродинамического сопротивления достижим при использовании в качестве паруса жесткого крыла. Этот тип вооружения все больше преобладает на гоночных катамаранах класса С. Применение жестких парусов на крейсерских судах затруднено необходимостью изменять площадь парусности в зависимости от ветровых условий. Другой возможностью снизить бA является увеличение площади парусов. Так как размеры парусов, которые могут быть приняты для судна заданных размерений и веса, связаны обратной зависимостью с величиной h — высотой центра давления, в качестве одного из решений может рассматриваться вооружение из двух мачт, разнесенных по ширине судна. Подобное вооружение использовались на сверхскоростных парусниках, строившихся для рекордных заездов: катамаранах Кроссбау II и Клифтон Флейшер. Пирамидальное вооружение является простейшим вариантом размещения парусов, не требующим большого числа вант и штагов. Возможно не очень привлекательное для гоночных судов, оно представляется весьма перспективным для крейсерских. Ходовые качества парусного судна зависят от выбора площади киля, оптимальной для имеющейся парусности. Несмотря на то, что шверцы на гоночных многокорпусных парусниках ‘устанавливаются редко, они имеют ряд преимуществ перед швертами. Вентиляцию шверцев – единственный их недостаток – можно предотвратить, если установить с наклоном вперед или использовать закрученные шверцы, так чтобы угол атаки погруженной части был ка 4° больше, чем на уровне ватерлинии. В немногих случаях, когда шверцы применялись на быстроходных судах, например на построенном Гужоном тримаране Фанки, результаты быля весьма обнадеживающими. Если говорить о способности судна держаться на курсе, что имеет первостепенное значение для плавания в открытом море, то хороший результат может быть получен при установке двух шверцев — в носовой н кормовой оконечностях. Та же задача успешно решается, вели вместо кормового шверца используется соответствующей площади плавник перед рулем, особенно в сочетании с двухмачтовым вооружением. Для крейсерских многокорпусных парусников на подводных крыльях время еще не пришло, но оно уже на подходе. Применение крыльев на тримаранах и, в особенности, проа для уменьшения сопротивления воды движению судна и крена показало их перспективность и с точки зрения мореходности. Эти потенциальные возможности недооцениваются в большинстве случаев, исключение представляют конструкции таких судов, как Мейфлай и Вилливо. Изложенные в этой книге соображения, возможно, помогут развитию работ в данном направлении, и в следующем поколения быстроходных парусников они найдут отражение.
Всеобщему признанию многокорпусных яхт в известной мере препятствует бытующее мнение с недостаточно обеспеченной безопасности по опрокидыванию. К сожалению, до настоящего времени проблема возвращения судна в положение на ровный киль после опрокидывания через борт окончательно не решена. С.Дж.Руис теоретически решил вопрос о переворачивании опрокинутого многокорпусного судна через носовые оконечности, но теория еще должна найти подтверждение в натурных испытаниях. Будем надеяться на их успех, ибо, как сказал Ф. Херешоф, самое интересное в плавании под парусом — это скорость.
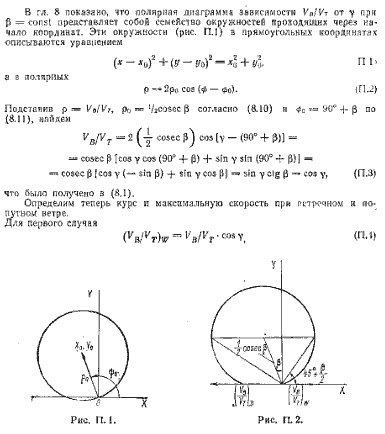

| a | ширина поперечной связи (3.2) расстояние между стойками крыльев (6.20) |
| А | удлинение паруса (4.5) площадь сечения поперечной связи (3.6) |
| АF | площадь подводного крыла (6.12) |
| АK | площадь киля (5.2) |
| АP | площадь вертикальной проекции корпуса (5.5) |
| АR | площадь руля (5.11) |
| АS | площадь паруса (4.1) |
| АW | площадь смоченной поверхности корпуса (6.12) |
| АF | площадь подводного крыла (6.12) |
| b | продольное расстояние между поперечными балками (3.9)
поперечное расстояние между центром давления паруса и центром продольного сопротивления (11.5) размах подводного крыла (6.20) |
| B | сила поддержания (6.1)
ширина по ватерлинии (2.6) |
| с | хорда (6.14) |
| CA | коэфф. аэродинамической силы (4.1) |
| CD | коэфф. сопротивления (4.3) |
| CDi | коэфф. индуктивного сопротивления (5.4) |
| CF | коэфф. трения (5.1) |
| CFo | коэфф. трения эквивалентной пластины (2.4) |
| CL | коэфф. подъемной силы (4.2) |
| CP | призматический коэфф. (2.17) |
| CPA | коэфф. аэродинамического сопротивления корпуса, рангоута, такелажа (8.6) |
| CW | коэфф. волнового сопротивления (2.16) |
| Cx | коэфф. продольной аэродинамической силы (8.18) |
| Cy | коэфф. поперечной аэродинамической силы (4.9) |
| CB | центр плавучести (центр величины) |
| CE | центр давления паруса |
| CG | центр тяжести |
| CLaR | центр бокового сопротивления |
| d | глубина воды
расстояние между центрами давления пирамидальных парусов (4.12) габаритная осадка (5.2) |
| DA | аэродинамическое сопротивление (1.6) |
| DH | гидродинамическое сопротивление (1.6) |
| DLR | отношение водоизмещения к длине (2.22) |
| Fr | число Фруда (2.9) |
| F | подъемная сила крыла (6.1) |
| FA | аэродинамическая сила (1.4) |
| fB | поперечная сила носового крыла (11.4) |
| FH | гидродинамическая сила (1.4) |
| fS | поперечная сила кормового крыла (11.4) |
| Fx | продольная составляющая аэродинамической силы (11.1) |
| Fy | поперечная составляющая аэродинамической силы (1.7) |
| g | ускорение силы тяжести (2.7) |
| G | модуль сдвига (3.7) |
| Gm | смоченный периметр сечения мидель-шпангоута (2.20) |
| h | расстояние по вертикали между центрами давления паруса CE и бокового сопротивления CLaR (1.7)
половина толщины поперечной связи (3.1) глубина погружения подводных крыльев (6.14) |
| H | осадка корпуса (2.6) |
| I | момент инерции площади (3.1) |
| l | длина поперечной балки (3.1)
продольное расстояние между кормовым крылом и CE (11.5) |
| L | длина по ватерлинии (2.2)
расстояние между носовым и кормовым крыльями (11.3) |
| L' | продольное расстояние от кормового крыла до CG (11.3) |
| LA | аэродинамическая подъемная сила (1.6) |
| LB | вертикальная сила носового крыла (11.2) |
| LH | гидродинамическая подъемная сила (1.6) |
| LS | вертикальная сила кормового крыла (11.2) |
| R | общее сопротивление (2.23) |
| Re | число Рейнольдса (2.2) |
| RF | сопротивление трения (2.1) |
| Ri | индуктивное сопротивление (5.5) |
| RW | волновое сопротивление (2.13) |
| S | размах крыла — высота паруса (4.5) |
| SLR | отношение скорости к длине корпуса |
| VA | скорость вымпельного ветра (1.1) |
| VB | скорость судна (1.1) |
| VA | скорость вымпельного ветра (1.1) |
| VT | скорость истинного ветра (1.1) |
| VW | скорость волны (2.8) |
| W | вес судна (1.7) |
| ȳ | поперечное расстояние между CLaR и CG (4.7) |
| ȳ' | поперечное расстояние от наветренного крыла до CLaR (6.9) |
| ž | вертикальное расстояние от CLaR до CG(4.7) |
| α | угол атаки (4.7) |
| αT | угол атаки, измеренный от угла нулевой подъемной силы (4.6) |
| β | курсовой угол относительно вымпельного ветра (1.2) |
| γ | курсовой угол относительно истинного ветра (1.2) |
| δA | угол аэродинамического сопротивления (1.5) |
| δH | угол гидродинамического сопротивления (1.5) |
| ε | отношение парусности судна к площади парусов (8.6) |
| ξ | амплитуда волны (2.7) |
| η | динамическая вязкость (2.2) |
| θ | угол крена (4.7)
угол наклона крыльев (6.1) |
| λ | длина волны (2.8) угол дрейфа (5.1) |
| ν | удельный вес (9.5) |
| ν1 | коэфф. скорости (8.18) |
| ν2 | коэфф. остойчивости (8.18) |
| ρA | массовая плотность воздуха (4.1) |
| ρH | массовая плотность воды (2.1) |
| σ | коэфф., учитывающий форму крыла в плане и его погружение (6.17) площадь мидель-шпангоута (2.16) |
| σmax | максимальное напряжение (3.1) |
| τ | толщина стенок (3.3) |
| ϕ | угол стреловидности крыльев (6.22) угол скручивания (3.7) |
| ψ | угол наклона паруса (4.12) |
| Ω | параметр, учитывающий влияние волнообразования на гидродинамические характеристики подводных ирыльев (6.15) |